Odpowiedź:
Przykładowe pełne rozwiązania
Sposób 1. (zastosowanie twierdzenia cosinusów)
Wykonamy rysunek pomocniczy (zobacz poniżej).
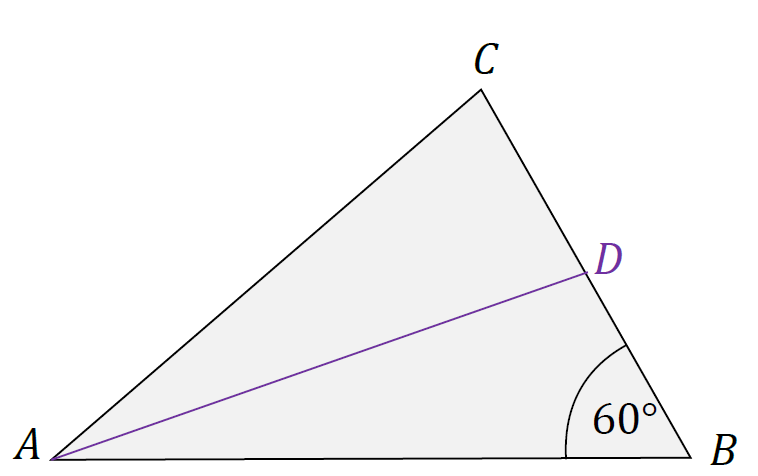
Ponieważ 𝐴𝐷 jest środkową, to |𝐵𝐷| = 4.
Do obliczenia długości środkowej |𝐴𝐷| zastosujemy twierdzenie cosinusów dla trójkąta 𝐴𝐵𝐷:
|𝐴𝐷|2 = |𝐴𝐵|2 + |𝐵𝐷|2 − 2 ⋅ |𝐴𝐵| ⋅ |𝐵𝐷| ⋅ cos |∡𝐴𝐵𝐶|
|𝐴𝐷|2 = 122 + 42 − 2 ⋅ 12 ⋅ 4 ⋅ 1⁄2 = 112
|𝐴𝐷| = √112 = 4√7
Sposób 2. (zastosowanie twierdzenia Pitagorasa i własności trójkąta o kątach 30°, 60°, 90°)
Wykonamy rysunek pomocniczy (zobacz poniżej).
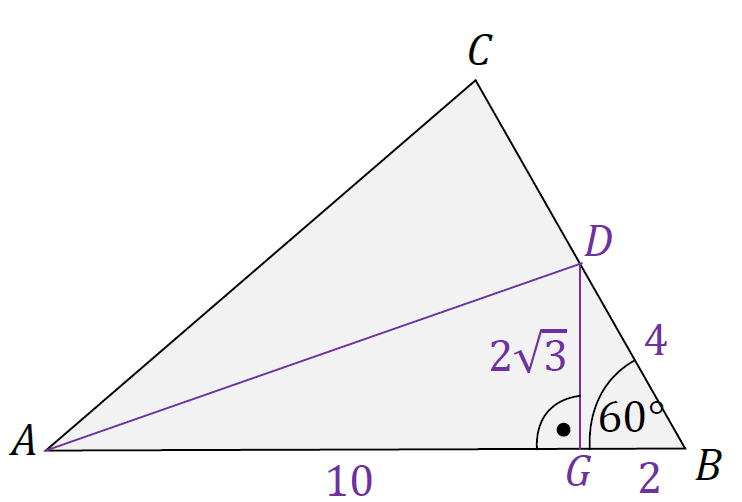
W celu obliczenia długości środkowej 𝐴𝐷 zastosujemy twierdzenie Pitagorasa dla trójkąta prostokątnego 𝐴𝐺𝐷.
Ponieważ 𝐴𝐷 jest środkową, to |𝐵𝐷| = 4. Rozważmy dalej trójkąt 𝐺𝐵𝐷. Trójkąt 𝐺𝐵𝐷 ma kąty o miarach: 30°, 60°,90°, skąd wynika, że przyprostokątne tego trójkąta mają
długości:
|𝐺𝐵| = 2 |𝐷𝐺| = 2√3
zatem długość przyprostokątnej 𝐴𝐺 trójkąta 𝐴𝐺𝐷 jest równa:
|𝐴𝐺| = 12 − 2 = 10
Obliczymy długość środkowej 𝐴𝐷 z twierdzenia Pitagorasa dla trójkąta 𝐴𝐺𝐷:
|𝐴𝐷|2 = |𝐴𝐺|2 + |𝐺𝐷|2
|𝐴𝐷|2 = 102 + (2√3)2 = 112
|𝐴𝐷| = √112 = 4√7
schemat punktacji
dla rozwiązania sposobem 1.
2 pkt – zapisanie poprawnego równania wynikającego z twierdzenia cosinusów dla trójkąta 𝐴𝐵𝐷 oraz prawidłowe obliczenie długości środkowej: |𝐴𝐷| = 4√7.
1 pkt – zapisanie równania wynikającego z twierdzenia cosinusów dla trójkąta 𝐴𝐵𝐷:
|𝐴𝐷|2 = |𝐴𝐵|2 + |𝐵𝐷|2 − 2 ⋅ |𝐴𝐵| ⋅ |𝐵𝐷| ⋅ cos |∡𝐴𝐵𝐶|
LUB
|𝐴𝐷|2 = 122 + 42 − 2 ⋅ 12 ⋅ 4 ⋅ cos 60°
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.
dla rozwiązania sposobem 2.
2 pkt – prawidłowe zastosowanie twierdzenia Pitagorasa dla trójkąta 𝐴𝐺𝐷 oraz prawidłowe obliczenie długości środkowej |𝐴𝐷| = 4√7.
1 pkt – wyodrębnienie trójkąta prostokątnego 𝐴𝐺𝐷 oraz trójkąta 𝐺𝐵𝐷 o kątach: 30°, 60°, 90°, łącznie z poprawnym określeniem długości jego boków: |𝐺𝐵| = 2, |𝐷𝐺| = 2√3.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.