Odpowiedź:
Przykładowe pełne rozwiązania
Sposób 1.
Przeanalizujemy zależności między odcinkami i kątami w przedstawionej sytuacji. Na
poniższych rysunkach pomocniczych przedstawimy graficzną ilustrację kroków postępowania.
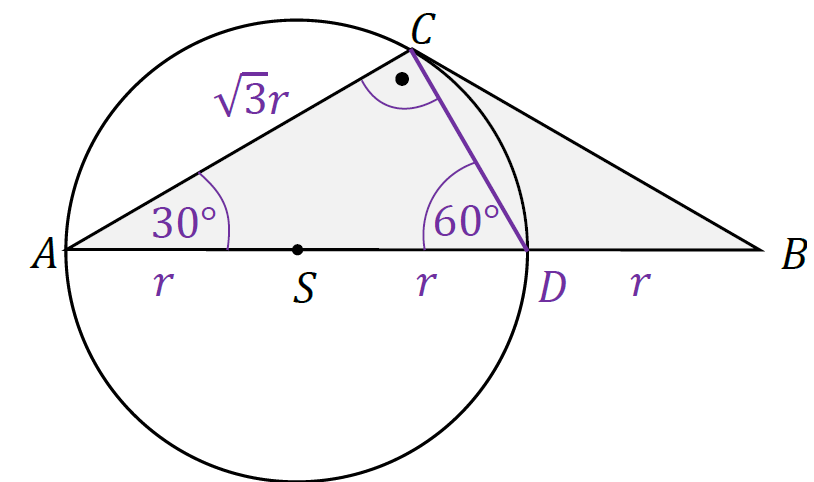
1. Kąt ∡𝐴𝐶𝐷 jest kątem wpisanym opartym na średnicy, zatem |∡𝐴𝐶𝐷| = 90°, czyli trójkąt
𝐴𝐷𝐶 jest prostokątny.
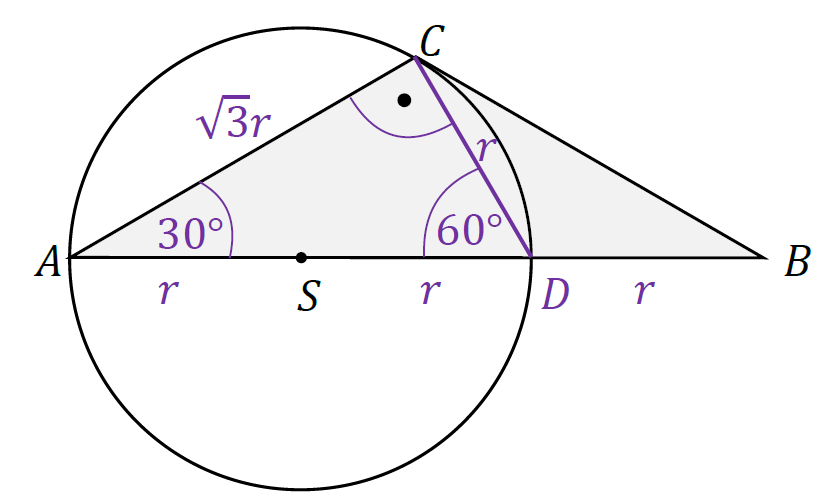
2. Zastosujemy twierdzenie Pitagorasa do obliczenia długości boku |𝐶𝐷|:
|𝐶𝐷|2 = |𝐴𝐷|2 − |𝐴𝐶|2 stąd |𝐶𝐷|2 = (2𝑟)2 − (√3𝑟)2 = 𝑟2
|𝐶𝐷| = 𝑟

3. Trójkąt 𝐴𝐷𝐶 o bokach 2𝑟, 𝑟, √3𝑟 jest połową trójkąta równobocznego, zatem:
|∡𝐶𝐴𝐷| = 30° , |∡𝐴𝐷𝐶| = 60°
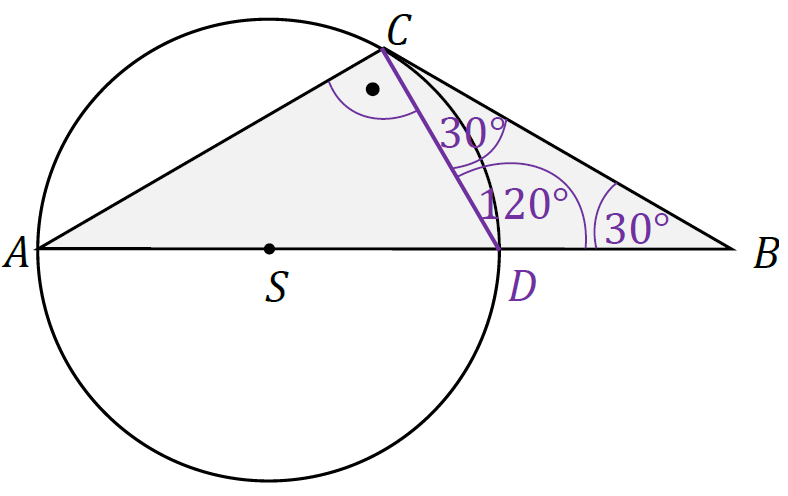
4. Zauważmy, że |𝐷𝐵| = |𝐷𝐶| = 𝑟, zatem trójkąt 𝐷𝐵𝐶 jest równoramienny. Z tego
i poprzedniego faktu wynika, że
|∡𝐶𝐷𝐵| = 180° − 60° = 120°, |∡𝐷𝐵𝐶| = 30°, |∡𝐵𝐶𝐷| = 30°
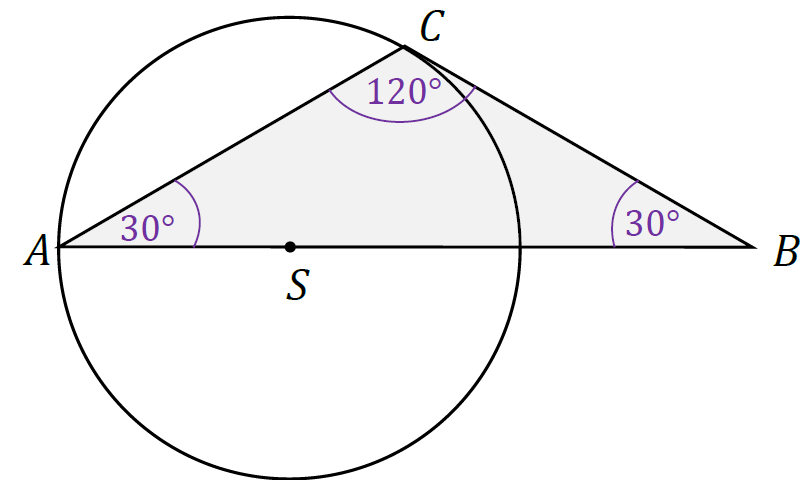
Z omówionych kroków 1.–4. wynika, że kąty w trójkącie 𝐴𝐵𝐶 mają miary:
|∡𝐶𝐴𝐵| = 30°, |∡𝐴𝐵𝐶| = 30°, |∡𝐵𝐶𝐴| = 120°
Sposób 2.
Przeanalizujemy zależności między odcinkami i kątami w przedstawionej sytuacji. Na
poniższych rysunkach pomocniczych przedstawimy graficzną ilustrację kroków postępowania.
1. Kąt ∡𝐴𝐶𝐷 jest kątem wpisanym opartym na średnicy, zatem |∡𝐴𝐶𝐷| = 90°.
2. Zauważmy, że: 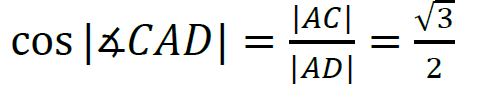
Stąd wynika, że |∡𝐶𝐴𝐷| = 30°, zatem |∡𝐴𝐷𝐶| = 60°.
3. Zauważamy, że |𝑆𝐶| = |𝑆𝐷| = 𝑟, czyli trójkąt 𝑆𝐷𝐶 jest równoramienny, zatem:
|∡𝐷𝐶𝑆| = |∡𝑆𝐷𝐶| = 60° Stąd wynika, że |∡𝐶𝑆𝐷| = 60°.
Z powyższego wynika, że trójkąt 𝑆𝐷𝐶 jest równoboczny.

4. Zauważamy, że |𝑆𝐴| = |𝑆𝐶| = 𝑟, czyli trójkąt 𝐴𝑆𝐶 jest równoramienny. Podobnie mamy |𝐷𝐵| = |𝐷𝐶| = 𝑟 , zatem trójkąt 𝐷𝐵𝐶 jest równoramienny. Z tych i poprzednich faktów wynika, że
|∡𝐴𝑆𝐶| = 180° − 60° = 120°, |∡𝑆𝐴𝐶| = 30°, |∡𝑆𝐶𝐴| = 30°
oraz
|∡𝐶𝐷𝐵| = 180° − 60° = 120°, |∡𝐷𝐵𝐶| = 30°, |∡𝐵𝐶𝐷| = 30°
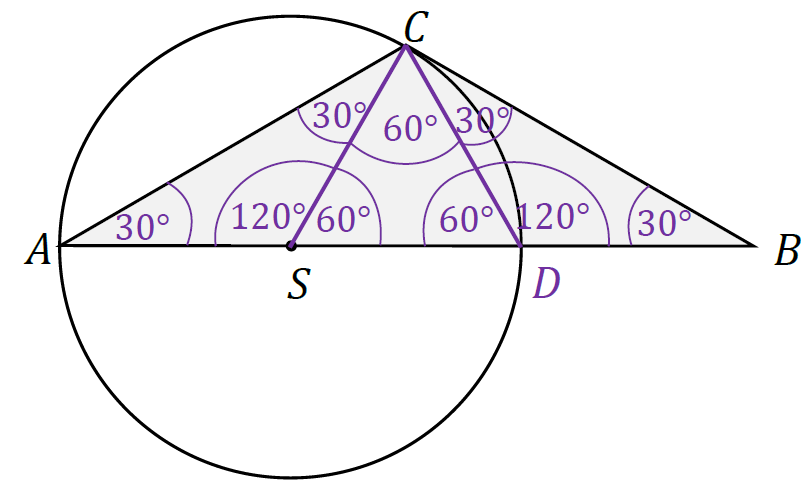
Z omówionych kroków 1.–4. wynika, że kąty w trójkącie 𝐴𝐵𝐶 mają miary:
|∡𝐶𝐴𝐵| = 30°, |∡𝐴𝐵𝐶| = 30°, |∡𝐵𝐶𝐴| = 120°
schemat punktacji
4 pkt – poprawne obliczenie miar kątów trójkąta 𝐴𝐵𝐶:
|∡𝐶𝐴𝐵| = 30°, |∡𝐴𝐵𝐶| = 30°, |∡𝐵𝐶𝐴| = 120°
3 pkt – poprawne obliczenie miar kątów w trójkącie 𝐷𝐵𝐶:
|∡𝐶𝐷𝐵| = 120°, |∡𝐷𝐵𝐶| = 30°, |∡𝐵𝐶𝐷| = 30°
LUB
– poprawne prawidłowe obliczenie miar kątów w trójkącie 𝐴𝑆𝐶:
|∡𝐴𝑆𝐶| = 120°, |∡𝐶𝐴𝑆| = 30°, |∡𝑆𝐶𝐴| = 30°.
2 pkt – poprawne obliczenie miar pozostałych kątów trójkąta 𝐴𝐷𝐶:
|∡𝐶𝐴𝐷| = 30°, |∡𝐴𝐷𝐶| = 60°
LUB
– poprawne obliczenie miar pozostałych kątów trójkąta 𝐵𝑆𝐶:
|∡𝑆𝐵𝐶| = 30°, |∡𝐶𝑆𝐵| = 60°
1 pkt – zapisanie, że kąt |∡𝐴𝐶𝐷| = 90°
LUB
– zapisanie, że kąt |∡𝐵𝐶𝑆| = 90°
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.