Odpowiedź:
Przykładowe pełne rozwiązania
Sposób 1.
Skorzystamy ze związków:

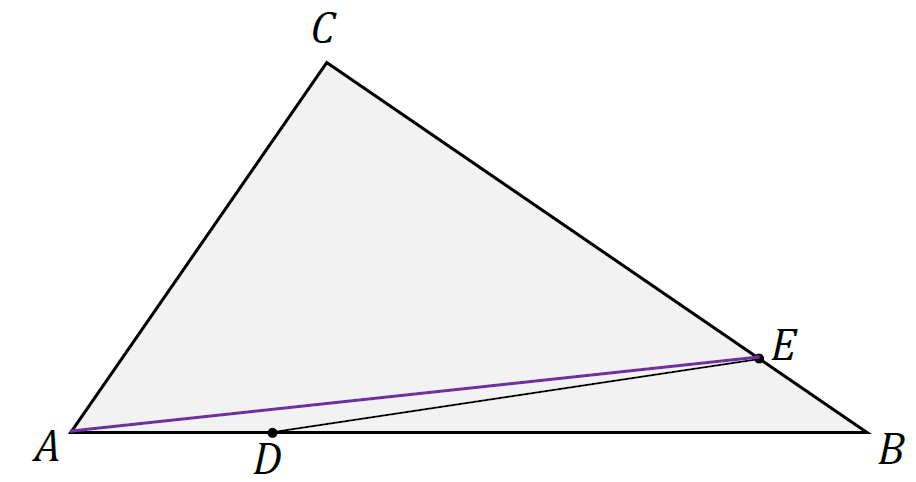
1. Zauważmy, że trójkąty 𝐴𝐵𝐸 i 𝐷𝐵𝐸 mają wspólny wierzchołek 𝐸, a ich podstawy 𝐷𝐵 i 𝐴𝐵 leżą na jednaj prostej. Zatem oba trójkąty mają tę samą wysokość opuszczoną
z wierzchołka 𝐸. Więc stosunek pól tych trójkątów jest równy stosunkowi długości ich
podstaw 𝐷𝐵 i 𝐴𝐵.
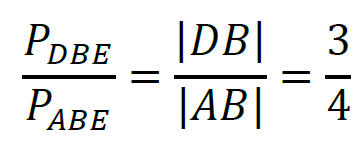
2. Trójkąty 𝐴𝐵𝐸 i 𝐴𝐵𝐶 mają wspólny wierzchołek 𝐴, a ich podstawy 𝐵𝐸 i 𝐵𝐶 leżą na jednaj prostej. Zatem oba trójkąty mają tę samą wysokość opuszczoną z wierzchołka 𝐴. Więc stosunek pól tych trójkątów jest równy stosunkowi długości ich podstaw 𝐵𝐸 i 𝐵𝐶.
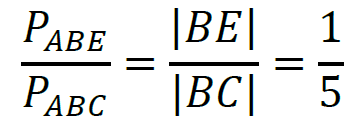
3. Z punktów 1. i 2. Otrzymujemy:
𝑃𝐷𝐵𝐸 = 3⁄4 𝑃𝐴𝐵𝐸 =
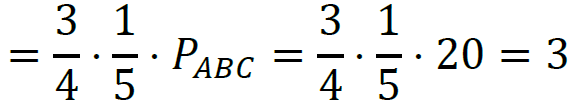
Sposób 2.
Oznaczmy miarę kąta ∡𝐷𝐵𝐸 = ∡𝐴𝐵𝐶 jako 𝛽.
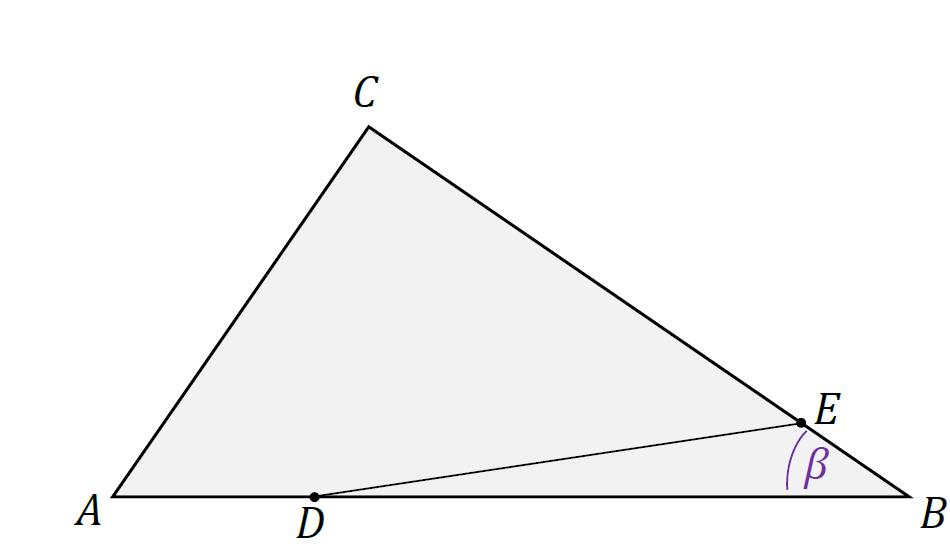
1. Zapiszemy wzór na pole trójkąta 𝐴𝐵𝐶 i wykorzystamy dane zadania:
𝑃𝐴𝐵𝐶 = 1⁄2 ⋅ |𝐴𝐵| ⋅ |𝐵𝐶| ⋅ sin 𝛽
20 = 1⁄2 ⋅ |𝐴𝐵| ⋅ |𝐵𝐶| ⋅ sin 𝛽 stąd |𝐴𝐵| ⋅ |𝐵𝐶| ⋅ sin 𝛽 = 40
2. Zapiszemy wzór na pole trójkąta 𝐷𝐵𝐸 i wykorzystamy warunek zadania:
𝑃𝐷𝐵𝐸 = 1⁄2 ⋅ |𝐷𝐵| ⋅ |𝐵𝐸| ⋅ sin 𝛽
𝑃𝐷𝐵𝐸 = 1⁄2 ⋅ ( 3⁄4 ⋅ |𝐴𝐵|) ⋅ ( 1⁄5 |𝐵𝐶|) ⋅ sin 𝛽 stąd 𝑃𝐷𝐵𝐸 = 3⁄40 ⋅ |𝐴𝐵| ⋅ |𝐵𝐶| ⋅ sin 𝛽
3. Do otrzymanego wzoru na pole trójkąta 𝐷𝐵𝐸 podstawimy wynik z punktu 1:
𝑃𝐷𝐵𝐸 = 3⁄40 ⋅ |𝐴𝐵| ⋅ |𝐵𝐶| ⋅ sin 𝛽 = 3⁄40 ⋅ 40 = 3
Sposób 3.
Wysokości trójkątów 𝐴𝐵𝐶 i 𝐷𝐵𝐸 opuszczone – odpowiednio – z wierzchołków 𝐶 i 𝐸 oznaczymy jako ℎ𝐶 , ℎ𝐸 .
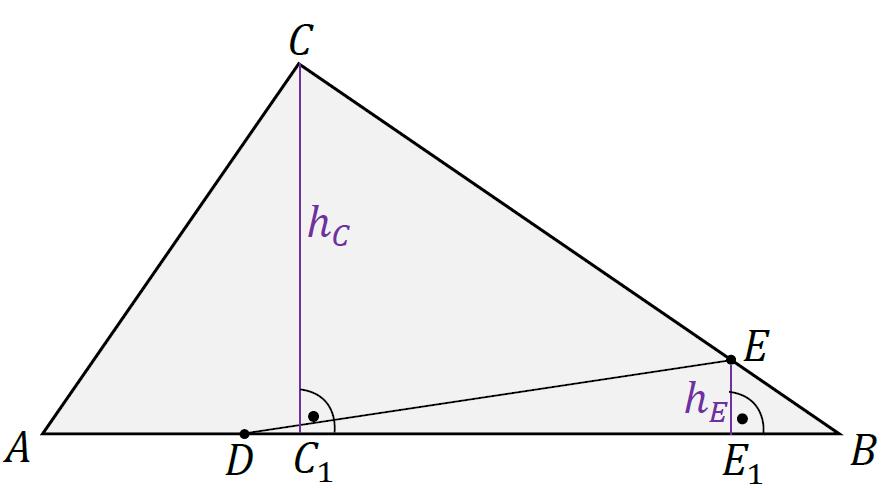
1. Zapiszemy wzór na pole trójkąta 𝐴𝐵𝐶 i wykorzystamy dane zadania:
𝑃𝐴𝐵𝐶 = 1⁄2 ⋅ |𝐴𝐵| ⋅ ℎ𝐶
20 = 1⁄2 ⋅ |𝐴𝐵| ⋅ ℎ𝐶 stąd |𝐴𝐵| ⋅ ℎ𝐶 = 40
2. Zapiszemy wzór na pole trójkąta 𝐷𝐵𝐸 i wykorzystamy warunek zadania:
𝑃𝐷𝐵𝐸 = 1⁄2 ⋅ |𝐷𝐵| ⋅ ℎ𝐸
𝑃𝐷𝐵𝐸 = 1⁄2 ⋅ ( 3⁄4 ⋅ |𝐴𝐵|) ⋅ ℎ𝐸 stąd 𝑃𝐷𝐵𝐸 = 3⁄8 ⋅ |𝐴𝐵| ⋅ ℎ𝐸
3. Trójkąty 𝐶1𝐵𝐶 oraz 𝐸1𝐵𝐸 są podobne (na podstawie cechy: kąt, kąt, kąt), zatem:
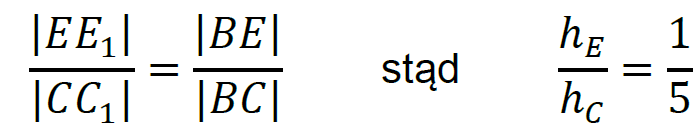
4. Do otrzymanego wzoru na pole trójkąta 𝐷𝐵𝐸 (punkt 2.) podstawimy wynik z punktu 1. i wynik z punktu 3.:
𝑃𝐷𝐵𝐸 = 3⁄8 ⋅ |𝐴𝐵| ⋅ ℎ𝐸 = 3⁄8 ⋅ |𝐴𝐵| ⋅ hC⁄5 = 3⁄40 ⋅ |𝐴𝐵| ⋅ ℎ𝐶 = 3⁄40 ⋅ 40 = 3
schemat punktacji
dla rozwiązania sposobem 1.
3 pkt – poprawna metoda obliczenia pola trójkąta 𝐷𝐵𝐸 oraz podanie wyniku: 𝑃𝐷𝐵𝐸 = 3.
2 pkt – wykazanie oraz zapisanie, że
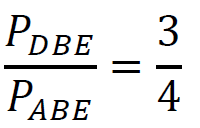 oraz
oraz 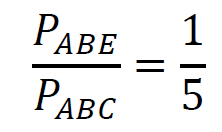
1 pkt – wykazanie i zapisanie, że stosunek pól trójkątów 𝐴𝐵𝐸 i 𝐷𝐵𝐸 jest równy stosunkowi długości ich podstaw 𝐷𝐵 i 𝐴𝐵:
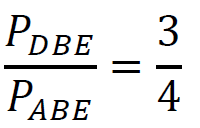
LUB
– wykazanie i zapisanie, że stosunek pól trójkątów 𝐴𝐵𝐸 i 𝐴𝐵𝐶 jest równy stosunkowi
długości ich podstaw 𝐵𝐸 i 𝐵𝐶:
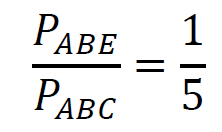
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.
dla rozwiązania sposobem 2.
3 pkt – poprawna metoda obliczenia pola trójkąta 𝐷𝐵𝐸 oraz podanie wyniku: 𝑃𝐷𝐵𝐸 = 3.
2 pkt – wyprowadzenie i zapisanie zależności |𝐴𝐵| ⋅ |𝐵𝐶| ⋅ sin 𝛽 = 40 oraz wzoru na pole
trójkąta 𝐷𝐵𝐸: 𝑃𝐷𝐵𝐸 = 1⁄2 ⋅ ( 3⁄4 ⋅ |𝐴𝐵|) ⋅ ( 1⁄5 |𝐵𝐶|) ⋅ sin 𝛽.
1 pkt – zastosowanie wzoru na pole trójkąta 𝐴𝐵𝐶 z sinusem kąta ∡𝐴𝐵𝐶 oraz wyprowadzenie zależności |𝐴𝐵| ⋅ |𝐵𝐶| ⋅ sin 𝛽 = 40
LUB
– zastosowanie wzoru na pole trójkąta 𝐷𝐵𝐸 z sinusem kąta ∡𝐷𝐵𝐸 oraz zapisanie /
zastosowanie związków |𝐷𝐵| = 3⁄4 |𝐴𝐵| oraz |BE| = 1⁄5 |𝐵𝐶|.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.
dla rozwiązania sposobem 3.
3 pkt – poprawna metoda obliczenia pola trójkąta 𝐷𝐵𝐸 oraz podanie wyniku: 𝑃𝐷𝐵𝐸 = 3.
2 pkt – zapisanie zależności |𝐴𝐵| ⋅ ℎ𝐶 = 40 oraz wzoru na pole trójkąta: 𝑃𝐷𝐵𝐸 = 3⁄8 ⋅ |𝐴𝐵| ⋅ ℎ𝐸 (lub równoważnego) oraz zapisanie zależności: ℎ𝐸 ⁄ℎC = 1⁄5 wynikającej z podobieństwa trójkątów 𝐶1𝐵𝐶 oraz 𝐸1𝐵𝐸 .
1 pkt – zastosowanie wzoru na pole trójkąta 𝐴𝐵𝐶 z wysokością ℎ𝐶 oraz wyprowadzenie
zależności |𝐴𝐵| ⋅ ℎ𝐶 = 40
LUB
– zastosowanie wzoru na pole trójkąta 𝐷𝐵𝐸 z wysokością ℎ𝐸 oraz zapisanie /
zastosowanie związku |𝐷𝐵| = 3⁄4 |𝐴𝐵|.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.