Odpowiedź:
Przykładowe pełne rozwiązania
Sposób 1.
1. Wysokości trzech trójkątów: 𝐶𝐴𝑊1, 𝐴𝐵𝑊2, 𝐶𝐵𝑊3, opuszczone z wierzchołków 𝑊1, 𝑊2, 𝑊3 oznaczymy odpowiednio jako: ℎ1, ℎ2, ℎ3. Zapiszemy wzory na pola powierzchni tych trójkątów:
𝑃1 = 1⁄2 ℎ1|𝐴𝐶| 𝑃2 = 1⁄2 ℎ2|𝐴B| 𝑃3 = 1⁄2 ℎ3|CB|
2. Zapiszemy związki wynikające z podobieństwa trójkątów:
Δ𝐶𝐴𝑊1 ∼ Δ𝐴𝐵𝑊2 zatem 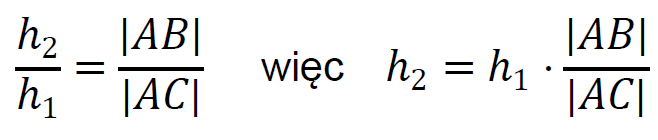
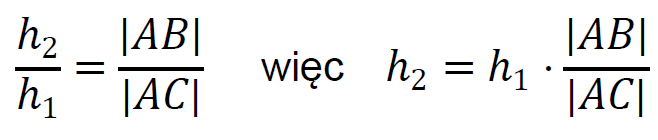
Δ𝐶𝐴𝑊1 ∼ Δ𝐶𝐵𝑊3 zatem 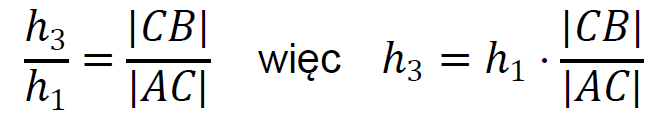
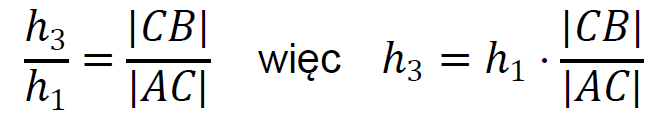
3. Ponownie zapiszemy wzory na pola trójkątów, wykorzystując powyższe zależności:
𝑃1 = 1⁄2 ℎ1|𝐴𝐶| 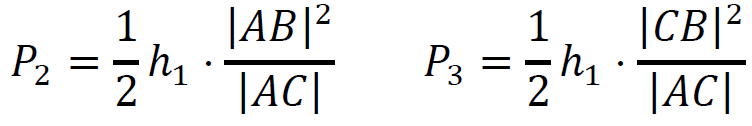
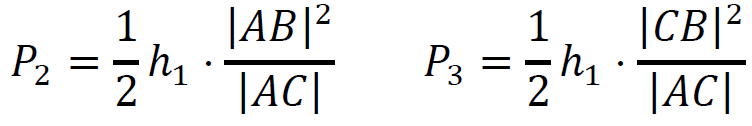
4. Obliczymy sumę 𝑃1 + 𝑃2.
𝑃1 + 𝑃2 =
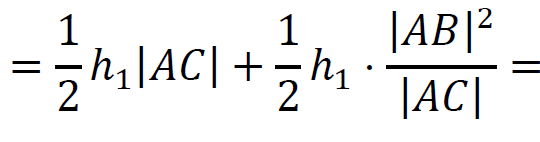
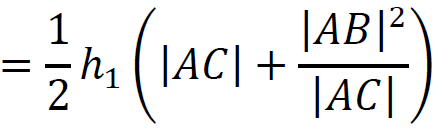
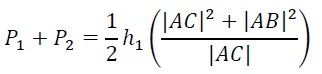
5. Wykorzystamy twierdzenie Pitagorasa dla trójkąta 𝐴𝐵𝐶:
Ponieważ
|𝐴𝐶|2 + |𝐴𝐵|2 = |𝐵𝐶|2
to
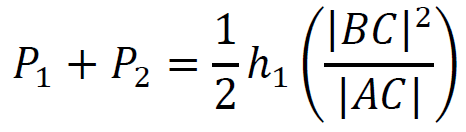
6. Prawa strona powyższego równania, na mocy pkt 3., jest równa 𝑃3:
𝑃1 + 𝑃2 = 𝑃3
To kończy dowód.
Sposób 2.
1. Wykorzystamy zależności między obwodami a polami figur płaskich podobnych:

2. Wykorzystamy fakt, że stosunki obwodów trójkątów podobnych są równe stosunkom
długości podstaw tych trójkątów:

3. Z zależności 1. i 2. wynika:


4. Obliczymy sumę 𝑃1 + 𝑃2:
𝑃1 + 𝑃2 =
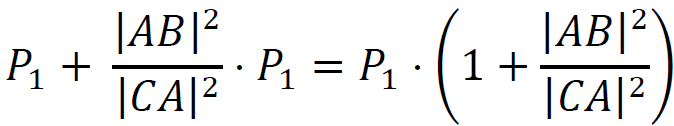
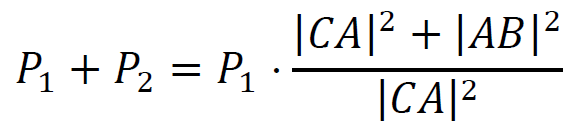
5. Skorzystamy z twierdzenia Pitagorasa dla trójkąta 𝐴𝐵𝐶:
|𝐶𝐴|2 + |𝐴𝐵|2 = |𝐵𝐶|2
Zatem równanie w drugim wierszu pkt 4. można zapisać w postaci:
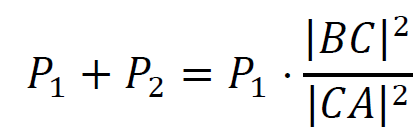
Prawa strona powyższego równania, na mocy pkt 3., jest równa 𝑃3:
𝑃1 + 𝑃2 = 𝑃3
To kończy dowód.
schemat punktacji
3 pkt – prawidłowe przeprowadzenie pełnego dowodu równania: 𝑃3 = 𝑃1 + 𝑃2.
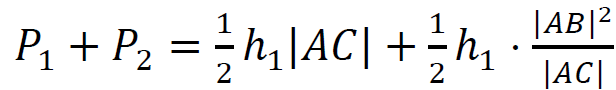
oraz zapisanie twierdzenia Pitagorasa dla trójkąta 𝐴𝐵𝐶: |𝐶𝐴|2 + |𝐴𝐵|2 = |𝐵𝐶|2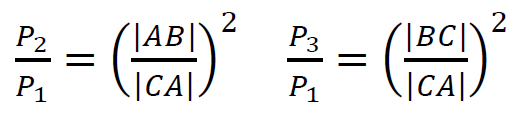 ,
,
zapisanie sumy pól figur płaskich wyrażonej za pomocą długości boków trójkąta i jednego z pól: 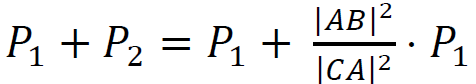
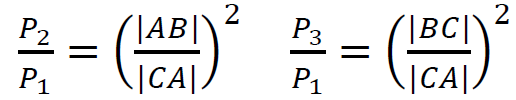 lub zależności równoważnych
lub zależności równoważnych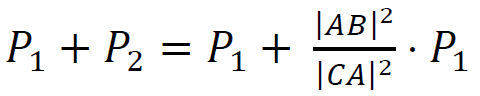 (lub równoważnie).
(lub równoważnie).
2 pkt – zapisanie sumy pól trójkątów 𝐶𝐴𝑊1, 𝐴𝐵𝑊2 wyrażonej poprzez wysokość jednego
z nich:
oraz zapisanie twierdzenia Pitagorasa dla trójkąta 𝐴𝐵𝐶: |𝐶𝐴|2 + |𝐴𝐵|2 = |𝐵𝐶|2
– zapisanie zależności między polami figur płaskich a długościami odcinków trójkąta:
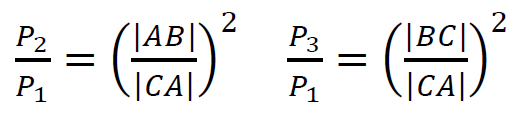 ,
, zapisanie sumy pól figur płaskich wyrażonej za pomocą długości boków trójkąta i jednego z pól:
oraz zapisanie twierdzenia Pitagorasa dla trójkąta 𝐴𝐵𝐶: |𝐶𝐴|2 + |𝐴𝐵|2 = |𝐵𝐶|2
LUB
– prawidłowe wyprowadzenie i zapisanie wyrażenia postaci: 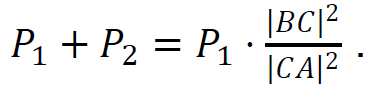
1 pkt – zapisanie wzorów na pola trójkątów oraz wyrażenie wysokości dwóch trójkątów (na mocy ich podobieństwa) poprzez wysokość trzeciego z nich, np.:
𝑃1 = 1⁄2 ℎ1|𝐴𝐶| 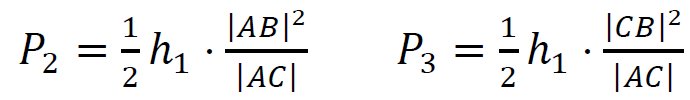
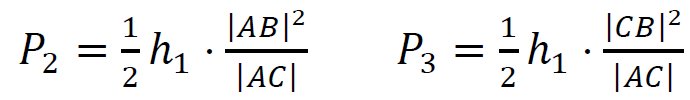
– zapisanie zależności między polami figur płaskich a długościami odcinków trójkąta, np.:
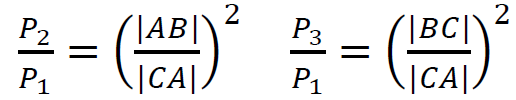 lub zależności równoważnych
lub zależności równoważnychLUB
– zapisanie sumy pól figur płaskich wyrażonej za pomocą długości boków trójkąta oraz
jednego z pól, np.:
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.