Odpowiedź:
Przykładowe pełne rozwiązania

Sposób 1.
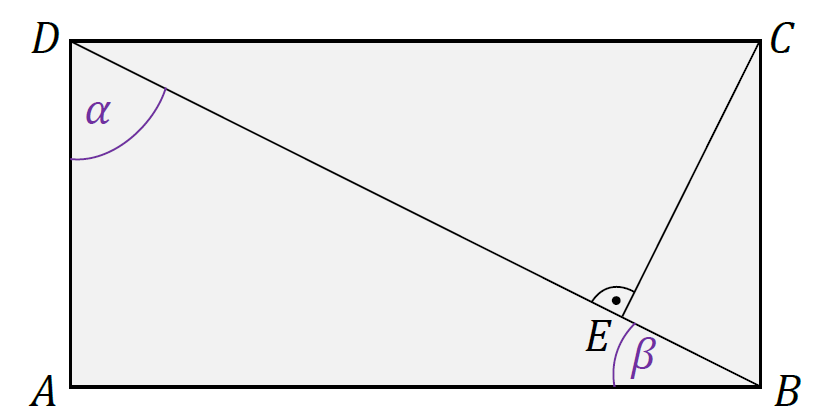
1. Wprowadzimy oznaczenia: ∡𝐵𝐷𝐴 = 𝛼, ∡𝐴𝐵𝐷 = 𝛽. To są kąty w trójkącie prostokątnym 𝐴𝐵𝐷, zatem: 𝛼 + 𝛽 = 90°


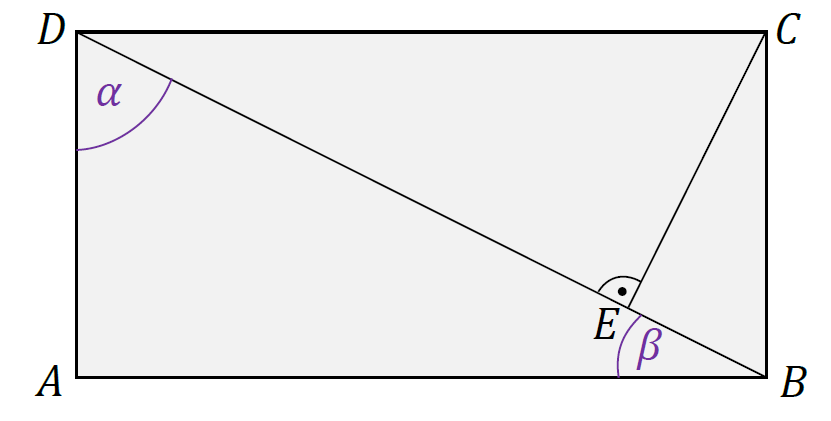
2. Wyodrębnimy trójkąty prostokątne: 𝐴𝐵𝐷, 𝐸𝐶𝐷. W tych trójkątach wyznaczymy kąty ostre. Skorzystamy z zależności, że 𝛼 + 𝛽 = 90° oraz z własności kątów naprzemianległych.

Na podstawie cechy: kąt, kąt, kąt, stwierdzamy, że trójkąty 𝐴𝐵𝐷, 𝐸𝐶𝐷 są podobne (zobacz rysunek poniżej).

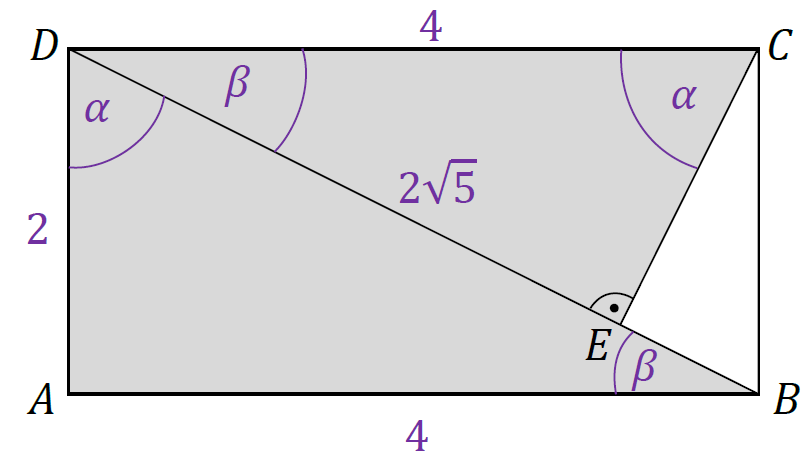
3. Ponieważ tg 𝛼 = 2 , to |𝐴𝐵| = 4. Zatem |𝐷𝐶| = 4.

4. Obliczymy |𝐵𝐷| z twierdzenia Pitagorasa dla trójkąta 𝐴𝐵𝐷:

|𝐵𝐷|2 = |𝐷𝐴|2 + |𝐴𝐵|2 = 22 + 42 = 20

|𝐵𝐷| = √20 = 2√5

5. Z podobieństwa trójkątów 𝐴𝐵𝐷, 𝐸𝐶𝐷 obliczymy długość odcinka 𝐸𝐶.

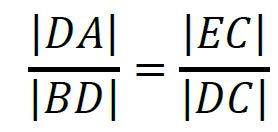36d.png zatem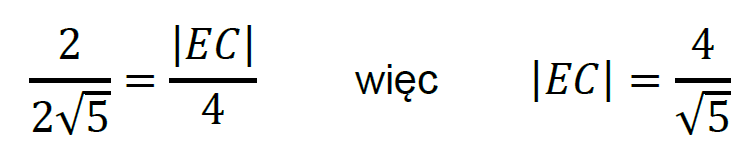
 



Sposób 2.
1. Zastosujemy oznaczenia: ∡𝐵𝐷𝐴 = 𝛼, ∡𝐴𝐵𝐷 = 𝛽. To są kąty w trójkącie prostokątnym 𝐴𝐵𝐷, zatem: 𝛼 + 𝛽 = 90°


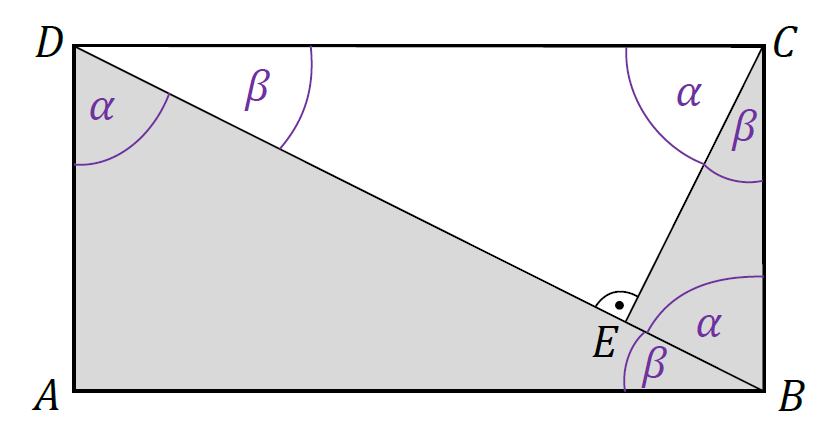
2. Wyodrębnimy trójkąty prostokątne: 𝐴𝐵𝐷, 𝐵𝐶𝐸, 𝐸𝐶𝐷. W tych trójkątach wyznaczymy kąty ostre. Skorzystamy z zależności, że 𝛼 + 𝛽 = 90° oraz z własności kątów naprzemianległych.

Na podstawie cechy: kąt, kąt, kąt, stwierdzamy, że trójkąty 𝐴𝐵𝐷, 𝐵𝐶𝐸, 𝐸𝐶𝐷 są podobne.

3. Z podobieństwa tych trójkątów wynika, że:

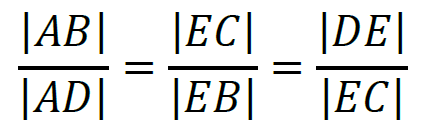zatem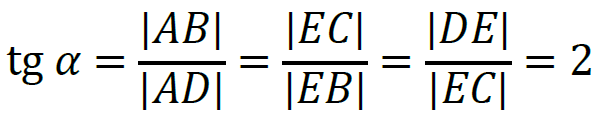


Wprowadzimy oznaczenie: |𝐸𝐶| = 𝑥. Długości boków 𝐸𝐵 i 𝐸𝐷 wyrazimy poprzez 𝑥. Z równań zapisanych powyżej otrzymujemy:

ponieważ |𝐴𝐷| = 2        to           |𝐴𝐵| = 4

ponieważ |𝐸𝐶| = 𝑥        to           |𝐸𝐵| = x⁄2 

ponieważ |𝐸𝐶| = 𝑥        to           |𝐸𝐷| = 2𝑥



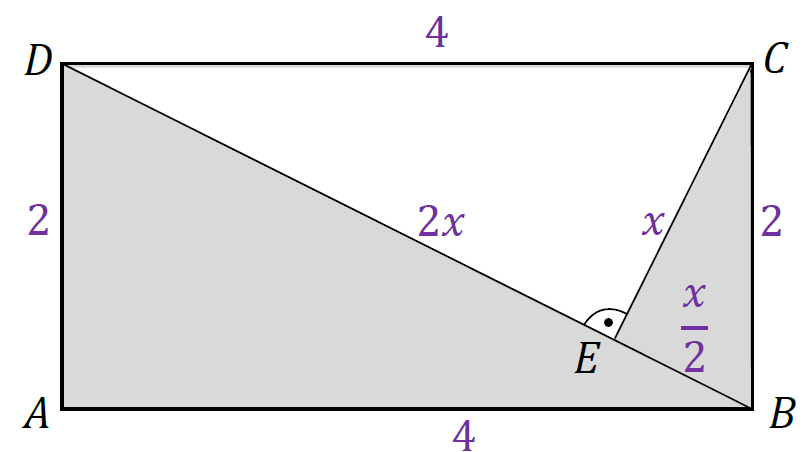
4. Zastosujemy twierdzenie Pitagorasa dla trójkąta 𝐸𝐶𝐷 (można zastosować alternatywnie dla trójkąta 𝐵𝐶𝐸):

𝑥2 + (2𝑥)2 = 42       więc 𝑥2 + 4𝑥2 = 16          stąd 5𝑥2 = 16 

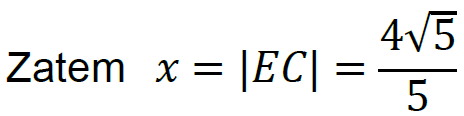
36j.png

schemat punktacji
3 pkt – prawidłowa metoda obliczenia długości odcinka 𝐸𝐶 oraz podanie prawidłowego
wyniku: 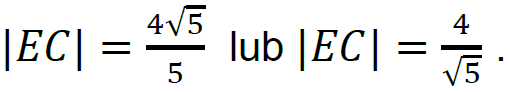36.1.png
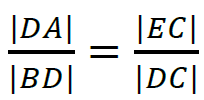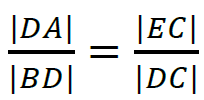2 pkt – zapisanie zależności 36.2.png oraz prawidłowe obliczenie z twierdzenia Pitagorasa długości odcinka 𝐵𝐷: |𝐵𝐷| = 2√5 (np. jak w sposobie 1. rozwiązania)
LUB
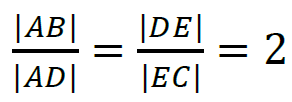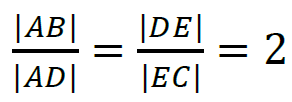– zapisanie zależności 36.4.png oraz zapisanie równania z jedną niewiadomą
wynikającego z twierdzenia Pitagorasa dla trójkąta 𝐷𝐸𝐶 (np. jak w sposobie 2.
rozwiązania)
LUB
– zapisanie zależności 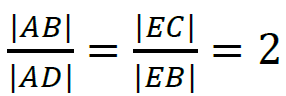36.5.png oraz zapisanie równania z jedną niewiadomą
wynikającego z twierdzenia Pitagorasa dla trójkąta 𝐵𝐶𝐸
LUB
– zapisanie równania z jedną niewiadomą, wyrażającą długość boku 𝐸𝐶, wynikającego
z twierdzenia Pitagorasa dla trójkąta 𝐷𝐸𝐶 lub 𝐵𝐶𝐸.

1 pkt – stwierdzenie, że trójkąty 𝐴𝐵𝐷 i 𝐷𝐸𝐶 (lub trójkąty 𝐴𝐵𝐷 i 𝐶𝐸𝐵) są podobne oraz
zapisanie zależności 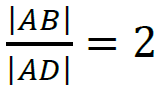36.6.png i obliczenie długości boku 𝐴𝐵: |𝐴𝐵| = 4.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.