Odpowiedź:
Przykładowe pełne rozwiązania
Sposób 1.
1. Zauważmy, że trójkąt 𝐴𝐶𝐵 jest równoramienny, gdzie: |𝐴𝐶| = |𝐶𝐵|.
Ta równość odcinków stycznych wynika z faktu, że trójkąty 𝑆𝐶𝐵 i 𝑆𝐶𝐴 są przystające na mocy cechy: kąt, bok (bok 𝐶𝑆), kąt (promień okręgu w punkcie styczności jest prostopadły do stycznej, a środek 𝑆 okręgu leży na dwusiecznej kąta ∡𝐴𝐶𝐵).
2. Zauważmy, że trójkąt 𝐴𝑆𝐷 jest równoramienny, gdzie: |𝑆𝐷| = |𝑆𝐴| (odcinki 𝑆𝐷 i 𝑆𝐴 są
promieniami okręgu).
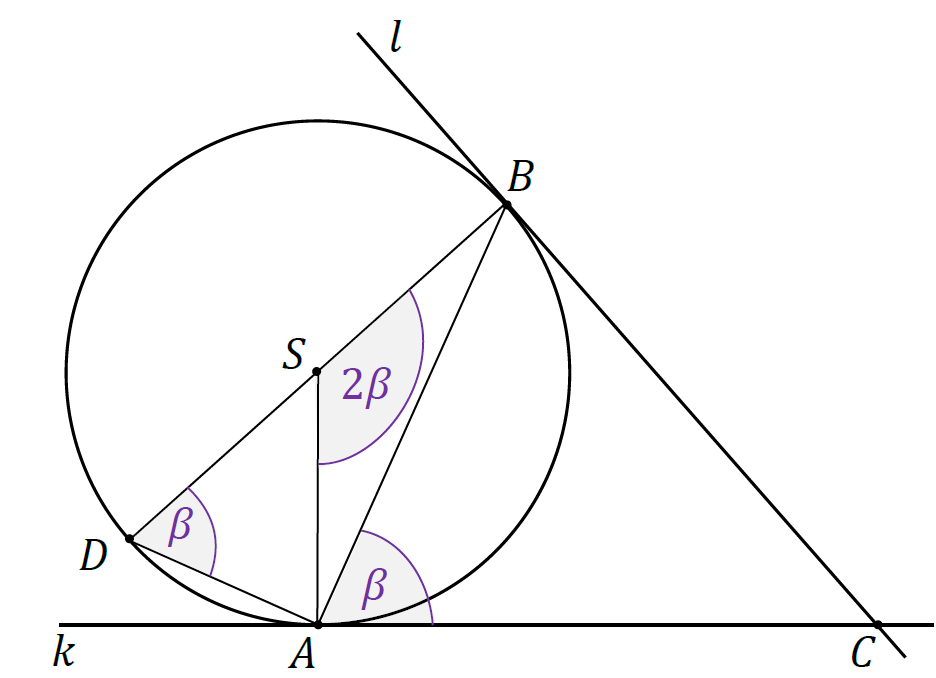
3. Sposób 1. kroku 3.
Oznaczymy |∡𝐵𝐴𝐶| = 𝛽. Na mocy twierdzenia o kącie między styczną a cięciwą i kącie środkowym opartym na tym łuku co cięciwa, mamy:
|∡𝐵𝑆𝐴| = 2𝛽.
Z twierdzenia o kącie wpisanym i środkowym otrzymujemy:
|∡𝐵𝐷𝐴| = 1⁄2 |∡𝐵𝑆𝐴| = 𝛽
Sposób 2. kroku 3.
Oznaczymy |∡𝐵𝐴𝐶| = 𝛽. Na mocy twierdzenia o kącie między styczną a cięciwą i kącie środkowym opartym na tym samym łuku co cięciwa, mamy:
|∡𝐵𝑆𝐴| = 2𝛽. Zatem:
Sposób 3. kroku 3.
Oznaczymy |∡𝐵𝐴𝐶| = 𝛽. Na mocy twierdzenia o kącie między styczną a cięciwą (tw. o kącie dopisanym) i kącie wpisanym opartym na tym samym łuku co cięciwa, mamy:
|∡𝐵𝐷𝐴| = |∡𝐵𝐴𝐶| = 𝛽
4. Ponieważ trójkąty 𝐴𝐶𝐵 oraz 𝐴𝑆𝐷 są równoramienne (zobacz pkt 1. i pkt 2.), stąd wynika, że:
|∡𝐶𝐵𝐴| = |∡𝐵𝐴𝐶| = 𝛽 |∡𝐴𝐶𝐵| = 180° − 2𝛽
|∡𝑆𝐷𝐴| = |∡𝐷𝐴𝑆| = 𝛽 |∡𝐴𝑆𝐷| = 180° − 2𝛽
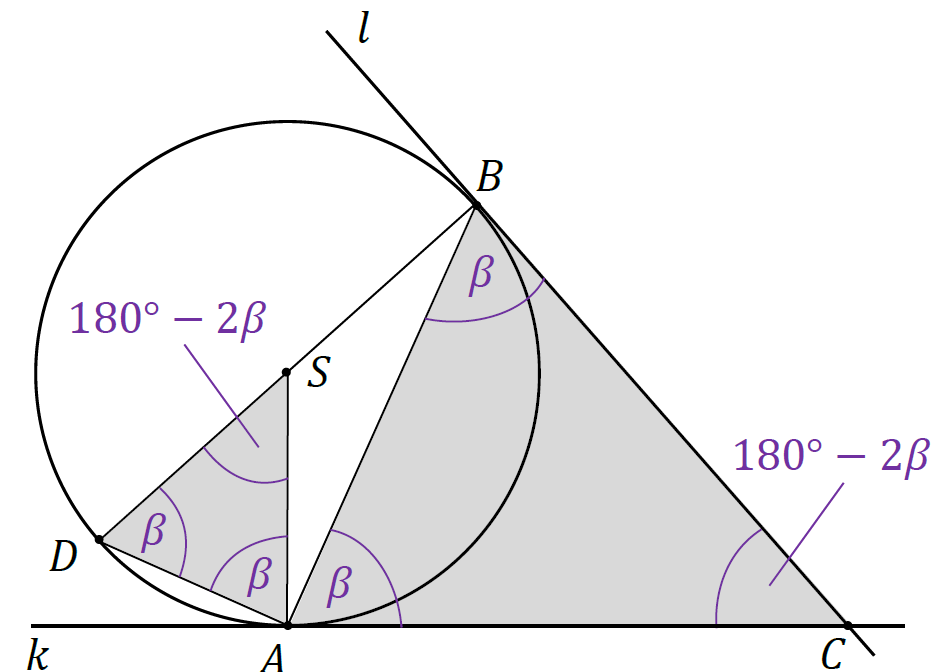
5. Trójkąty 𝐴𝐶𝐵 i 𝐴𝑆𝐷 są podobne na mocy cechy: kąt, kąt, kąt.
Sposób 2.
1. Zauważmy, że trójkąt 𝐴𝐶𝐵 jest równoramienny, gdzie:
|𝐴𝐶| = |𝐶𝐵|
Powyższa równość odcinków stycznych wynika z faktu, że trójkąty 𝑆𝐶𝐵 i 𝑆𝐶𝐴 są przystające na mocy cechy: kąt, bok (𝐶𝑆), kąt (promień okręgu w punkcie styczności jest prostopadły do stycznej, a środek 𝑆 okręgu leży na dwusiecznej kąta ∡𝐴𝐶𝐵).
2. Miarę kąta ∡𝐴𝐶𝐵 oznaczymy jako 𝛼. Ponieważ suma kątów wewnętrznych trójkąta jest równa 180°, a trójkąt 𝐴𝐶𝐵 jest równoramienny, to:
|∡𝐵𝐴𝐶| = |∡𝐶𝐵𝐴| = 𝛽
Zatem
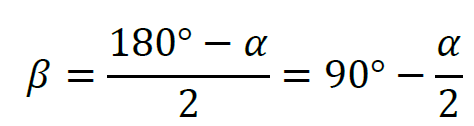
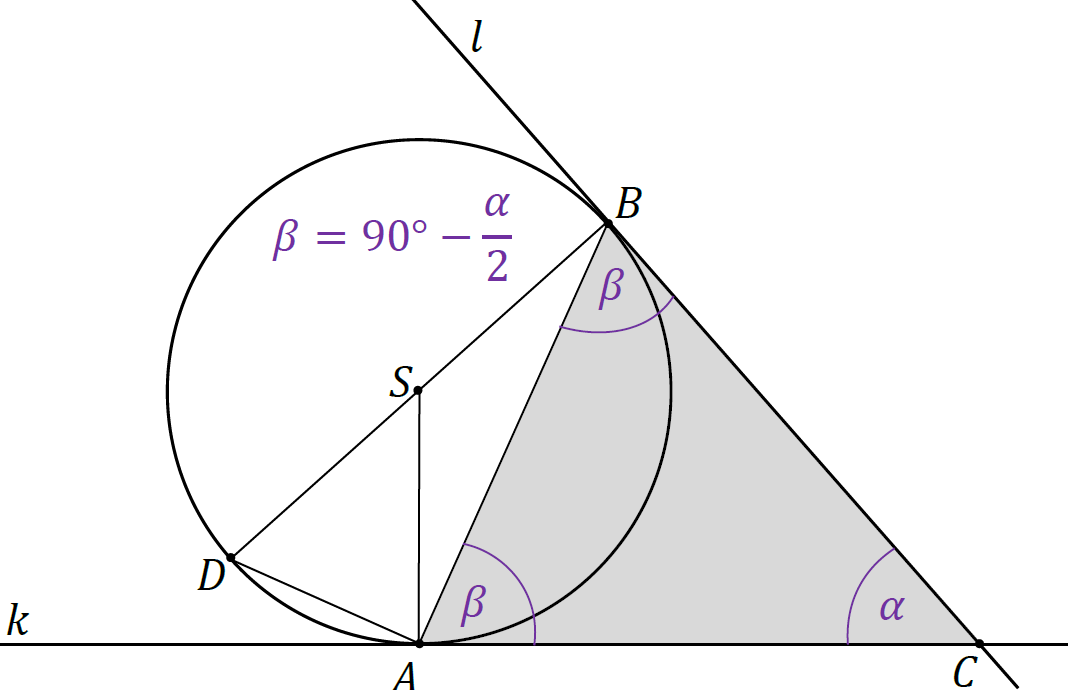
3. Rozważmy czworokąt 𝐴𝐶𝐵𝑆. Miarę kąta ∡𝐵𝑆𝐴 oznaczymy przez 𝛾. Ponieważ suma kątów w czworokącie jest równa 360°, a kąty ∡𝑆𝐴𝐶 oraz ∡𝐶𝐵𝑆 są proste, to:
|∡𝐵𝑆𝐴| = 360° − |∡𝑆𝐴𝐶| − |∡𝐶𝐵𝑆 | − |∡𝐴𝐶𝐵|
Zatem:
𝛾 = 360° − 90° − 90° − 𝛼
𝛾 = 180° − 𝛼
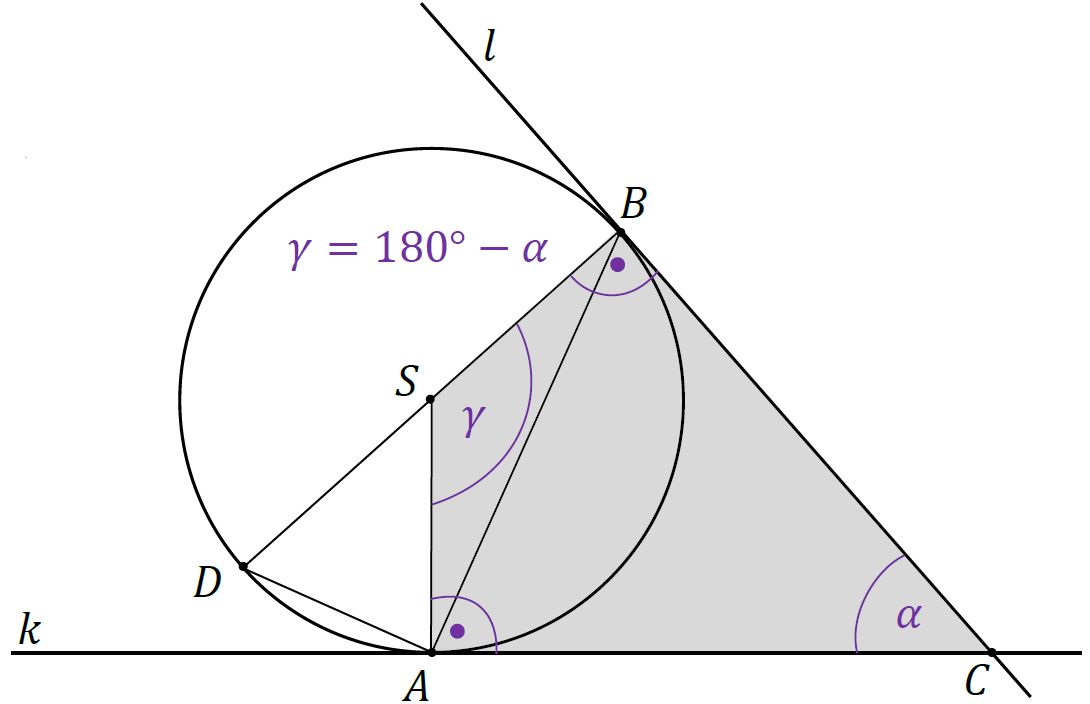
4. Kąt ∡𝐴𝑆𝐷 jest przyległy do kąta ∡𝐵𝑆𝐴, zatem:
|∡𝐴𝑆𝐷| = 180° − 𝛾
|∡𝐴𝑆𝐷| = 180° − (180° − 𝛼)
|∡𝐴𝑆𝐷| = 𝛼
5. Zauważmy, że trójkąt 𝐴𝑆𝐷 jest równoramienny, gdzie |𝑆𝐷| = |𝑆𝐴| (odcinki 𝑆𝐷 i 𝑆𝐴 są promieniami okręgu). Zatem:
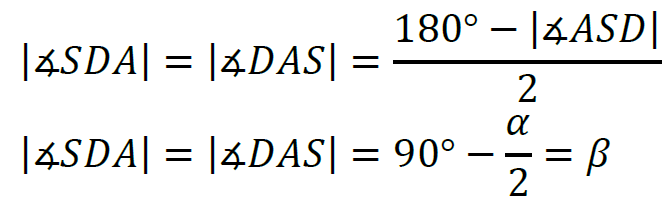
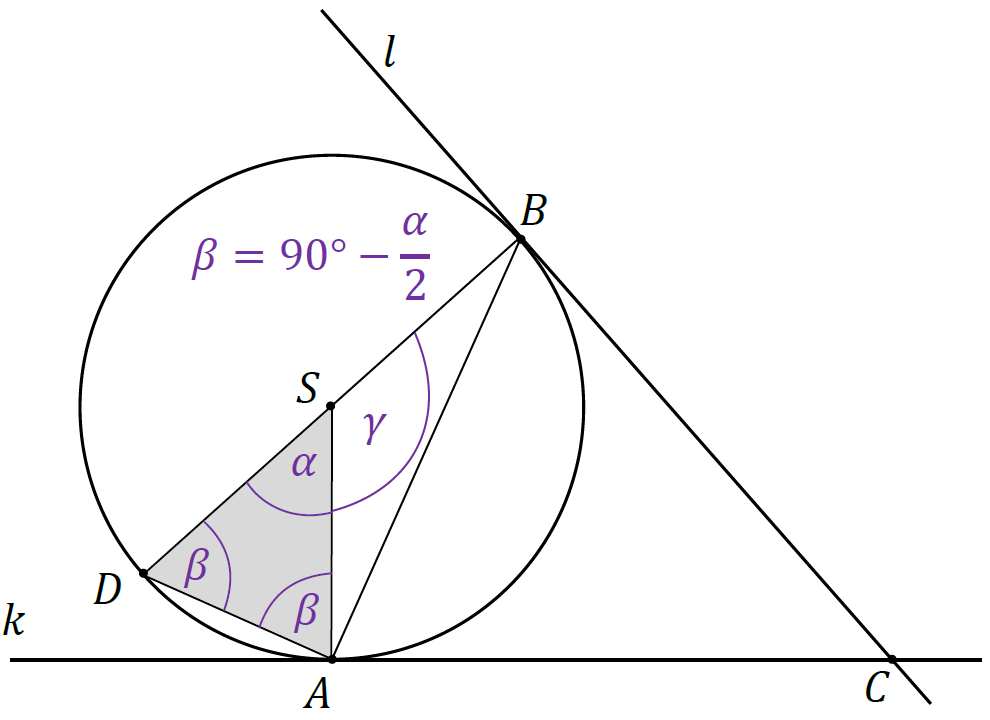
Uwaga! Miarę kąta ∡𝐵𝐷𝐴 (czyli 𝛽) można było wyrazić poprzez miarę kąta ∡𝐵𝑆𝐴 (czyli 𝛾) na mocy twierdzenia o kącie środkowym opartym na tym samym łuku (tutaj łuku 𝐴𝐵) co kąt wpisany: 𝛾 = 2𝛽
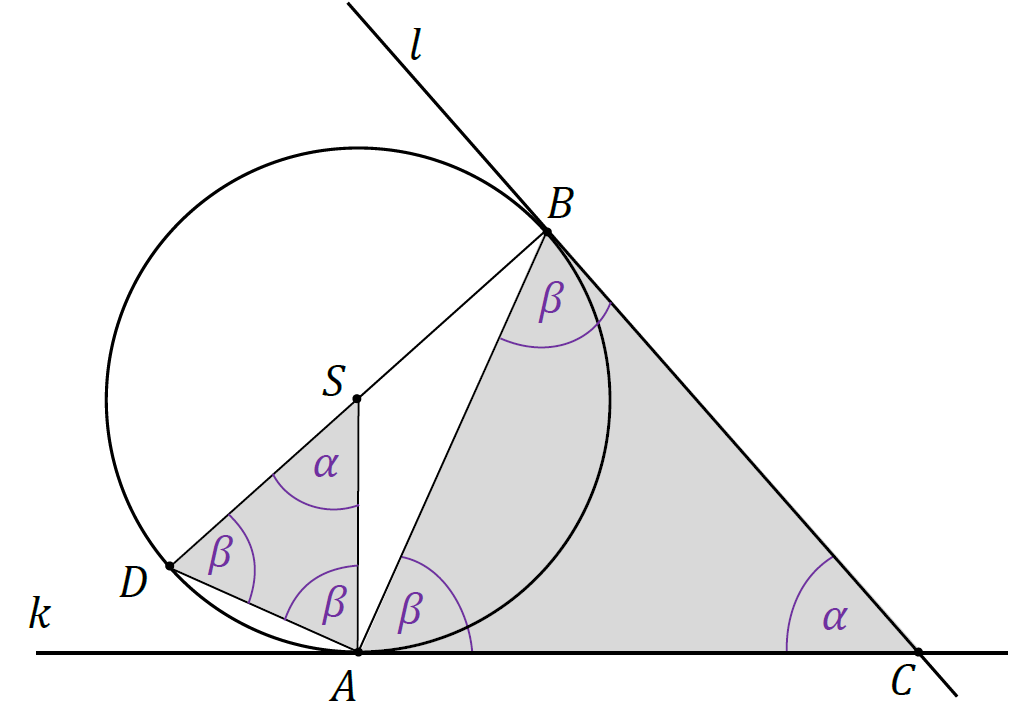
6. Trójkąty 𝐴𝐶𝐵 i 𝐴𝑆𝐷 są podobne na mocy cechy: kąt, kąt, kąt.
schemat punktacji
(uwzględniające oba sposoby rozwiązania oraz ich kompilacje)
3 pkt – poprawne przeprowadzenie pełnego dowodu podobieństwa trójkątów 𝐴𝐶𝐵 i 𝐴𝑆𝐷.
2 pkt – zapisanie związków pomiędzy kątami: |∡𝐵𝑆𝐴| = 180° − |∡𝐴𝐶𝐵| oraz |∡𝐴𝑆𝐷| = 180° − |∡𝐵𝑆𝐴| oraz zapisanie zależności wymienionych w kryterium za 1 pkt
LUB
– wykazanie, że |∡𝐴𝑆𝐷| = |∡𝐴𝐶𝐵| oraz zapisanie zależności wymienionych w kryterium za 1 pkt
LUB
– wykazanie, że |∡𝐵𝐷𝐴| = |∡𝐵𝐴𝐶| oraz zapisanie zależności wymienionych w kryterium za 1 pkt.
1 pkt – zapisanie, że trójkąt 𝐴𝐶𝐵 jest równoramienny oraz zapisanie związku między jego kątami wewnętrznymi: |∡𝐵𝐴𝐶| = |∡𝐶𝐵𝐴| = (180° − |∡𝐴𝐶𝐵|): 2
LUB
– zapisanie, że trójkąt 𝐴𝑆𝐷 jest równoramienny oraz zapisanie związku między jego
kątami wewnętrznymi: |∡𝑆𝐷𝐴| = |∡𝐷𝐴𝑆| = (180° − |∡𝐴𝑆𝐷|): 2
LUB
– zapisanie, ze trójkąty 𝐴𝐶𝐵 i 𝐴𝑆𝐷 są równoramienne, oraz wskazanie / zapisanie
równości odpowiednich ramion.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.