Odpowiedź:
Przykładowe pełne rozwiązanie
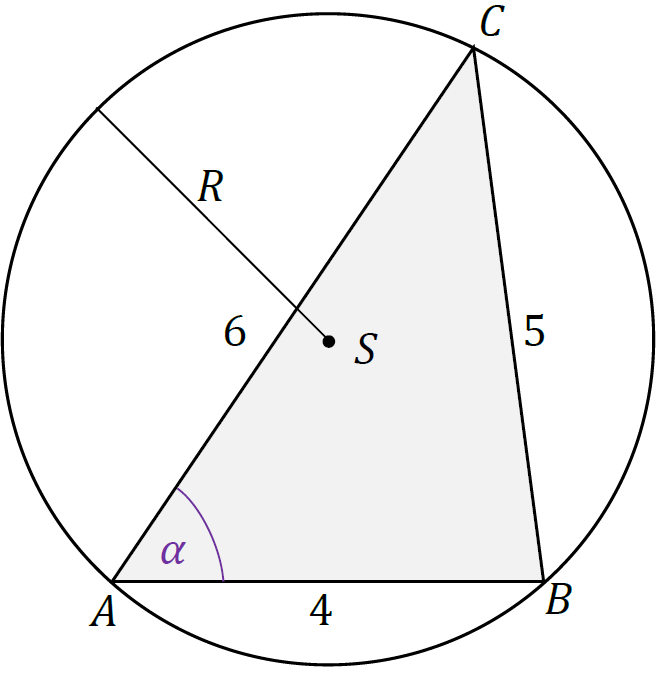
W celu obliczenia promienia okręgu opisanego na trójkącie zastosujemy twierdzenie sinusów oraz twierdzenie cosinusów. Z twierdzenia cosinusów wyznaczymy cosinus wybranego kąta w trójkącie, następnie dla tego kąta oraz boku naprzeciwko tego kąta zastosujemy twierdzenie sinusów.
1. Wprowadzimy oznaczenie: |∡𝐶𝐴𝐵| = 𝛼. Z twierdzenia cosinusów obliczymy cos 𝛼:
|𝐵𝐶|2 = |𝐴𝐶|2 + |𝐴𝐵|2 − 2 ⋅ |𝐴𝐶| ⋅ |𝐴𝐵| ⋅ cos 𝛼
52 = 62 + 42 − 2 ⋅ 6 ⋅ 4 ⋅ cos 𝛼
25 = 36 + 16 − 48 ⋅ cos 𝛼
48 ⋅ cos 𝛼 = 52 − 25
cos 𝛼 = 27⁄48 = 9⁄16
2. Z „jedynki trygonometrycznej” obliczymy sin 𝛼:
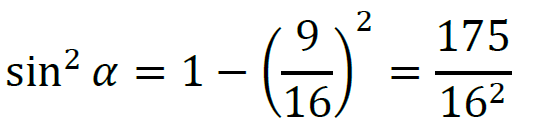
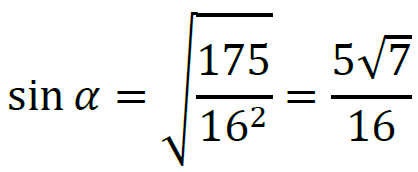
3. Zastosujemy twierdzenie sinusów do obliczenia promienia okręgu opisanego na trójkącie 𝐴𝐵𝐶:
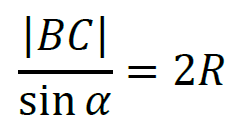
zatem
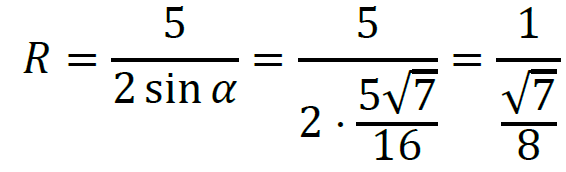
więc
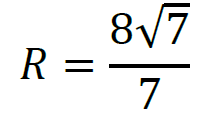
schemat punktacji
3 pkt – poprawna metoda obliczenia promienia okręgu opisanego na trójkącie oraz podanie prawidłowego wyniku: 𝑅 = 8√7⁄7
2 pkt – obliczenie sinusa jednego z kątów w trójkącie (np. ∡𝐶𝐴𝐵)
LUB
– obliczenie cosinusa jednego z kątów w trójkącie (np. ∡𝐶𝐴𝐵) oraz poprawne zapisanie dwóch równań wynikających z twierdzenia sinusów oraz „jedynki trygonometrycznej” dla jednego z kątów w trójkącie (tego samego).
1 pkt – obliczenie cosinusa jednego z kątów w trójkącie (np. ∡𝐶𝐴𝐵)
LUB
– poprawne zapisanie dwóch równań wynikających z twierdzenia cosinusów oraz twierdzenia sinusów dla jednego z kątów w trójkącie (tego samego, np. ∡𝐶𝐴𝐵).
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.