Odpowiedź:
Przykładowe pełne rozwiązania
Sposób 1.
(rozwiązanie układu równań złożonego z równań prostych 𝑘 i 𝑘⊥)
1. Oznaczmy przez 𝑘⊥ prostą prostopadłą do prostej 𝑘. Punkt styczności okręgu 𝒪 i prostej 𝑘 jest punktem przecięcia się prostej 𝑘 z prostą 𝑘⊥ prostopadłą do niej i przechodzącą przez środek tego okręgu. Należy rozwiązać układ równań złożony z równań obu tych prostych.
Rysunek poglądowy.
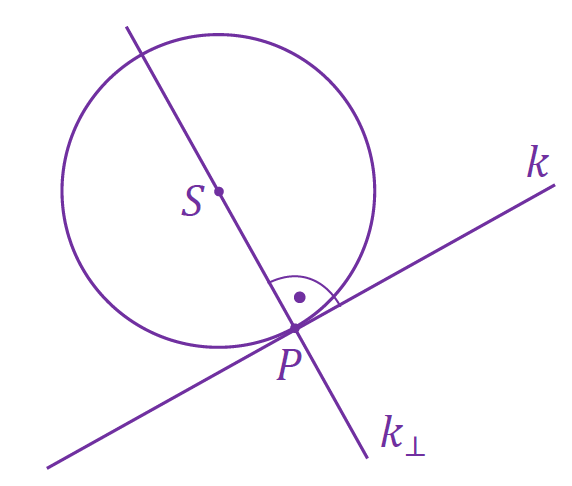
2. Wyznaczymy równanie prostej 𝑘⊥– prostopadłej do 𝑘 i przechodzącej przez punkt 𝑆:
𝑘: 𝑦 = 2𝑥 − 11
Prosta 𝑘⊥ ma równanie:
𝑘⊥: 𝑦 = − 1⁄2x + 𝑏
Punkt 𝑆 = (3, −4) należy do prostej 𝑘⊥ , zatem:
− 4 = − 1⁄2 ⋅ 3 + 𝑏 stąd 𝑏 = − 5⁄2 , więc prosta 𝑘⊥ ma równanie:
𝑘⊥: 𝑦 = − 1⁄2 x − 5⁄2
3. Rozwiążemy układ równań:
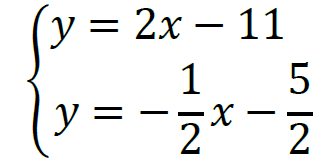
− 1⁄2 x − 5⁄2 = 2𝑥 − 11 stąd − 5⁄2 x = − 17⁄2 więc 𝑥 = 17⁄5
𝑦 = 2𝑥 − 11 = 2 ⋅ 17⁄5 − 11 = − 21⁄5
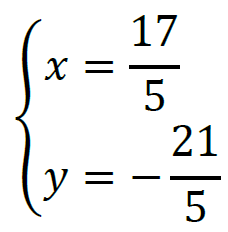
zatem 𝑃 = ( 17⁄5 , − 21⁄5 )
Sposób 2.
(rozwiązanie układu równań złożonego z równania prostej 𝑘 i równania okręgu 𝒪)
Uwaga!
Sposób 1. rozwiązania zadania 41.2. jest niezależny od rozwiązania zadania 41.1. Natomiast sposób 2. pokazuje takie rozwiązanie zadania 41.2., w którym zdający może wykorzystać rozwiązanie zadania 41.1.
Współrzędne punktu styczności prostej 𝑘 i okręgu 𝒪 są rozwiązaniami układu równań,
w którym jedno jest równaniem okręgu 𝒪, a drugie jest równaniem prostej 𝑘. Zapiszemy i rozwiążemy ten układ równań. Wykorzystamy wyznaczone w zadaniu 41.1. równanie okręgu
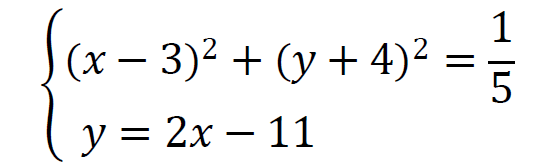
(𝑥 − 3)2 + (2𝑥 − 11 + 4)2 = 1⁄5 zatem (𝑥 − 3)2 + (2𝑥 − 7)2 = 1⁄5
𝑥2 − 6𝑥 + 9 + 4𝑥2 − 28𝑥 + 49 − 1⁄5 = 0
5𝑥2 − 34𝑥 + 289⁄5 = 0
𝑥 = 34⁄10 = 17⁄5
𝑦 = 2𝑥 − 11 = 2 ⋅ 17⁄5 − 11 = − 21⁄5
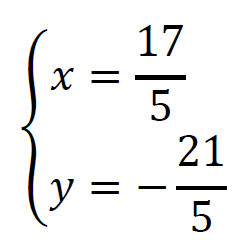więc 𝑃 = ( 17⁄5 , − 21⁄5 )schemat punktacji
Zasady oceniania
(dla rozwiązania sposobem 1.)
2 pkt – zapisanie układu złożonego z poprawnych równań prostych 𝑘 i 𝑘⊥ oraz prawidłowe rozwiązanie tego układu i zapisanie wyniku: 𝑥 = 17⁄5 , 𝑦 = − 21⁄5
1 pkt – poprawna metoda wyznaczenia równania prostej prostopadłej do 𝑘 i przechodzącej
przez punkt 𝑆 oraz zapisanie równania prostej 𝑘⊥: 𝑦 = − 1⁄2 x − 5⁄2
LUB
– zapisanie równania prostej prostopadłej do 𝑘 i przechodzącej przez punkt 𝑆,
z poprawną wartością współczynnika kierunkowego tej prostej i błędną wartością wyrazu wolnego, oraz zapisanie układu złożonego z równań prostych 𝑘 i 𝑘⊥.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.
(dla rozwiązania sposobem 2.)
2 pkt – zapisanie układu złożonego z równania prostej 𝑘 i równania okręgu 𝒪 oraz rozwiązanie tego układu równań i zapisanie wyniku: 𝑥 = 17⁄5 , 𝑦 = − 21⁄5
1 pkt – zapisanie układu równań, w którym jedno jest równaniem prostej 𝑘, a drugie jest
równaniem okręgu (𝑥 − 3)2 + (𝑦 + 4)2 = 1⁄5
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.