Odpowiedź do zadania

Odpowiedź:

Przykładowe pełne rozwiązanie

Wprowadzimy oznaczenia dla odcinków (jak na rysunku poniżej) – długości krawędzi prostopadłościanu oznaczymy przez 𝑎, 𝑏, 𝑐, a przekątną prostopadłościanu i przekątną ściany 𝐵𝐶𝐺𝐹 oznaczymy przez 𝑑 oraz 𝑒. Warunki zadania zapiszemy jako:

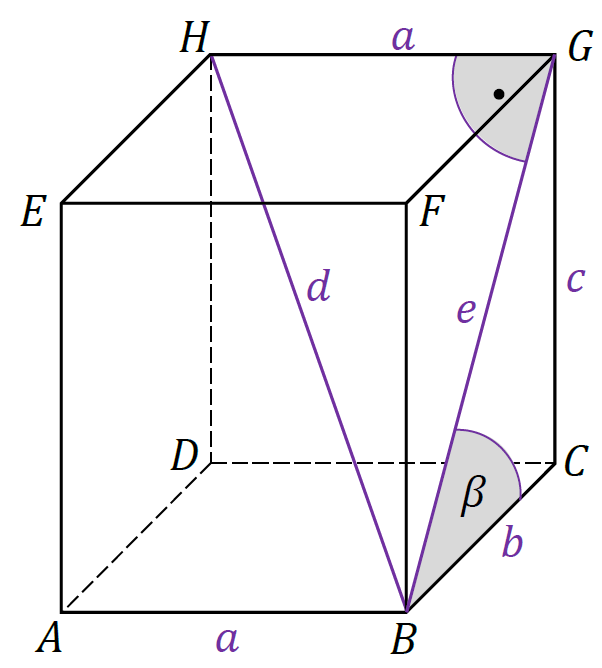
tg 𝛽 = ⁹⁄₇ e = 2 ⋅ √130 d = 2 ⋅ √194

1. Wyznaczymy zależność między 𝑏 a 𝑐 w trójkącie 𝐵𝐶𝐺:

tg 𝛽 = ^c⁄_b = ⁹⁄₇ stąd 𝑐 = ⁹⁄₇ b

2. Zastosujemy twierdzenie Pitagorasa dla trójkąta prostokątnego 𝐵𝐶𝐺, w celu obliczenia 𝑏 i 𝑐:

𝑏² + 𝑐² = 𝑒²

^{Wykorzystamy związek z pkt. 1:}

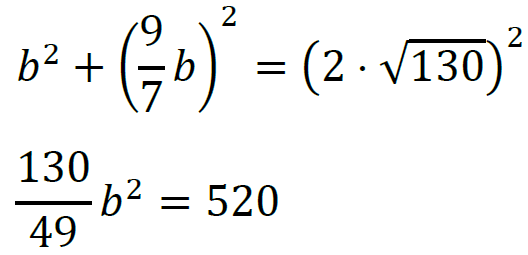
𝑏² = 196

zatem

𝑏 = 14 oraz 𝑐 = ⁹⁄₇ ⋅ 14 = 18

3. Zauważmy, że trójkąt 𝐵𝐺𝐻 jest prostokątny (kąt prosty jest przy wierzchołku 𝐺). Zastosujemy twierdzenie Pitagorasa dla trójkąta prostokątnego 𝐵𝐺𝐻, w celu obliczenia 𝑎.

𝑒² + 𝑎² = 𝑑²

(2 ⋅ √130)² + 𝑎² = (2 ⋅ √194)²

𝑎² = 256

𝑎 = 16

4. Obliczymy pole powierzchni całkowitej prostopadłościanu:

𝑃_𝑐 = 2𝑎𝑏 + 2𝑏𝑐 + 2𝑎𝑐

𝑃_𝑐 = 2 ⋅ 16 ⋅ 14 + 2 ⋅ 14 ⋅ 18 + 2 ⋅ 16 ⋅ 18

𝑃_𝑐 = 1528

schemat punktacji

4 pkt – poprawna metoda obliczenia pola powierzchni całkowitej graniastosłupa oraz podanie prawidłowego wyniku: 𝑃𝑐 = 1528.

3 pkt – poprawne obliczenie długości wszystkich krawędzi prostopadłościanu: |𝐵𝐶| = 14,

|𝐶𝐺| = 18, |𝐺𝐻| = 16

LUB

– poprawna metoda obliczenia długości wszystkich krawędzi prostopadłościanu, błąd rachunkowy w obliczeniach i poprawne zapisanie wzoru na pole powierzchni całkowitej prostopadłościanu.

2 pkt – obliczenie długości dwóch krawędzi: |𝐵𝐶| = 14, |𝐶𝐺| = 18 oraz zapisanie równania wynikającego z twierdzenia Pitagorasa dla trójkąta 𝐵𝐺𝐻: |𝐵𝐺|² + |𝐺𝐻|² = |𝐻𝐵|²

LUB

– obliczenie długości krawędzi: |𝐺𝐻| = 16 oraz zapisanie równania wynikającego z twierdzenia Pitagorasa dla trójkąta 𝐵𝐶𝐺:

|𝐵𝐶|² + |𝐶𝐺|² = |𝐵𝐺|² i zapisanie związku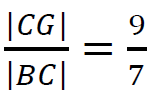

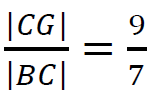
1 pkt – zapisanie równania wynikającego z twierdzenia Pitagorasa dla trójkąta 𝐵𝐶𝐺:

|𝐵𝐶|² + |𝐶𝐺|² = |𝐵𝐺|² oraz zapisanie związku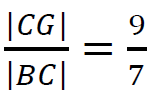

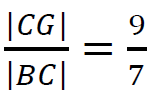
LUB

– zauważenie, że trójkąt 𝐵𝐺𝐻 jest prostokątny, i zapisanie równania wynikającego z twierdzenia Pitagorasa dla trójkąta 𝐵𝐺𝐻: |𝐵𝐺|² + |𝐺𝐻|²= |𝐻𝐵|²

^LUB

– zapisanie równania 𝑎² + 𝑏² + 𝑐² = 𝑑² (lub z innymi oznaczeniami), gdzie 𝑎, 𝑏, 𝑐, 𝑑 są oznaczeniami odpowiednich odcinków w prostopadłościanie (zobacz przykładowe rozwiązanie).

0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.