Odpowiedź:
Przykładowe pełne rozwiązania
Wprowadzimy oznaczenia:
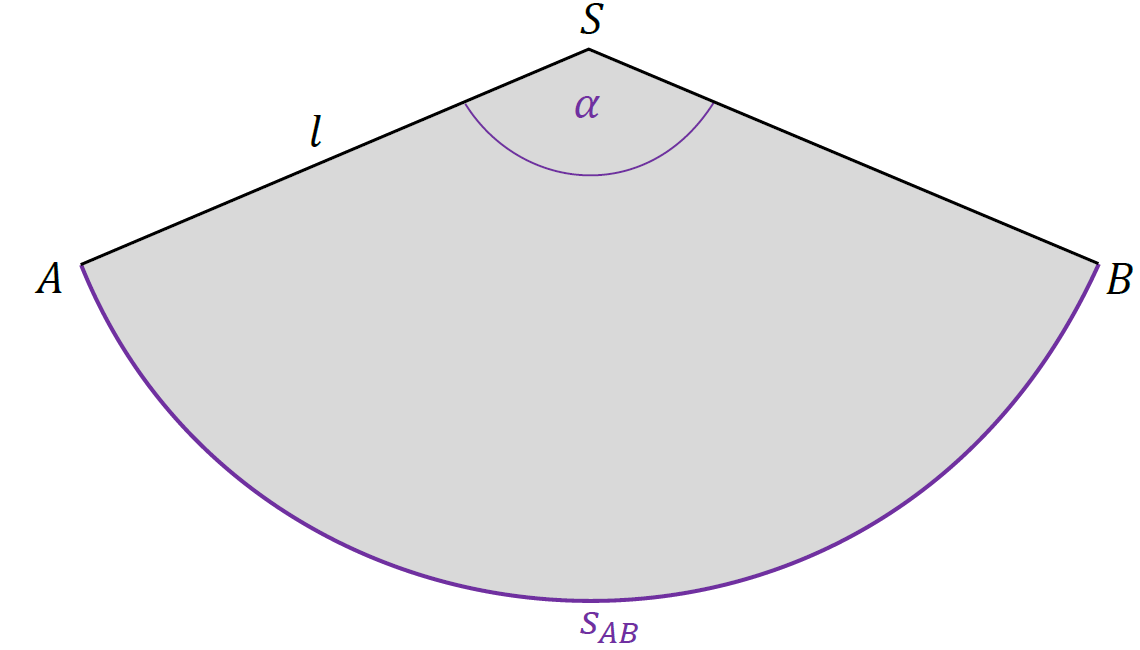
𝑠𝐴𝐵 – długość łuku 𝐴𝐵 wycinka koła 𝐴𝐵𝑆.
𝑃𝐴𝐵𝑆 – pole wycinka koła 𝐴𝐵𝑆.
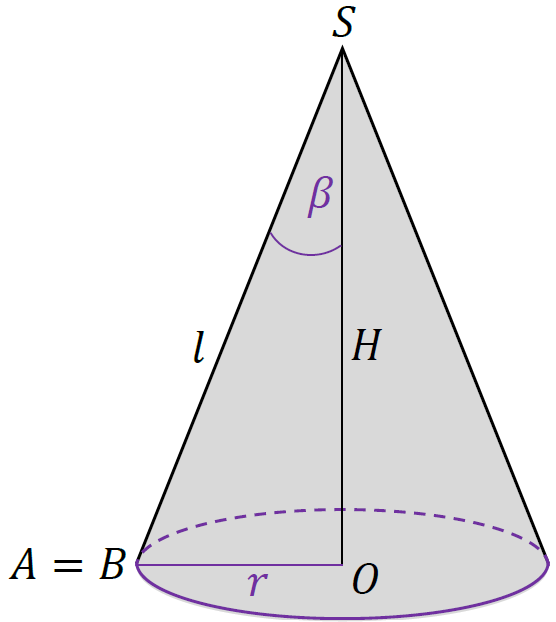
𝑟 = d⁄2 – promień okręgu w podstawie stożka.
𝛼 = |∡𝐵𝑆𝐴| – miara kąta ∡𝐵𝑆𝐴 wycinka koła.
𝛽 – połowa miary kąta rozwarcia stożka.
Sposób 1.
Wyprowadzimy wzór końcowy na symbolach danych (pominiemy obliczenia pośrednie).
1. Zauważmy, że z łuku 𝐴𝐵 wycinka koła powstał okrąg w podstawie stożkowej czapeczki. Zatem długość łuku 𝐴𝐵 jest równa długości (obwodowi) okręgu w podstawie stożka. Zastosujemy wzór na długość łuku 𝐴𝐵 oraz wzór na obwód okręgu:
𝑠𝐴𝐵 = Obwpodstawy
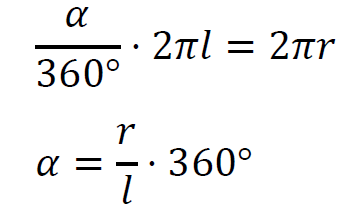
Uwaga
Zauważmy, że otrzymany wzór zadaje nadzwyczaj prostą relację między kątem wycinka koła i kątem rozwarcia stożka:
𝛼 = sin 𝛽 ⋅ 360°
2. Wyrazimy 𝑙 poprzez 𝐻 i 𝑑 na podstawie twierdzenia Pitagorasa:
𝑙2 = 𝐻2 + 𝑟2
zatem
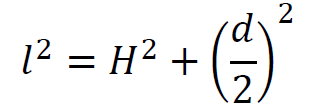
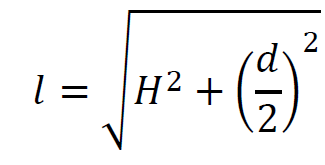
3. Zapiszemy wzór na miarę kąta 𝛼 i ją obliczymy:
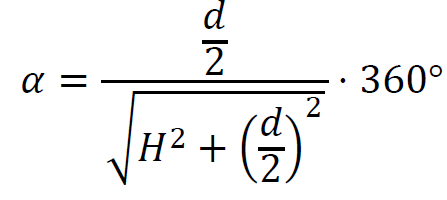
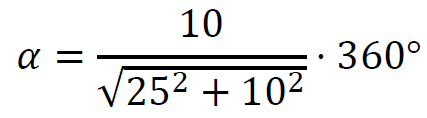
𝛼 ≈ 134°
Sposób 2.
Wyprowadzimy wzór końcowy na symbolach danych (pominiemy obliczenia pośrednie).
1. Zauważmy, że pole 𝐴𝐵𝑆 wycinka koła jest równe polu powierzchni bocznej stożka (polu powierzchni czapeczki). Zastosujemy wzór na pole 𝐴𝐵𝑆 wycinka koła oraz wzór na pole powierzchni bocznej stożka:
𝑃𝐴𝐵𝑆 = 𝑃𝑏
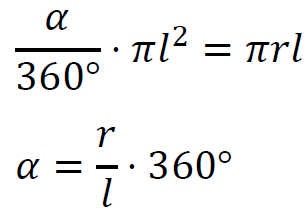
Krok 2. i 3. Jak w sposobie 1.
schemat punktacji
3 pkt – poprawna metoda obliczenia miary kąta ∡𝐵𝑆𝐴 (lub wyprowadzenie równania na miarę kąta: 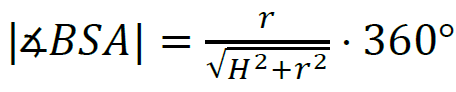 ) oraz podanie prawidłowego wyniku ∡𝐵𝑆𝐴 ≈ 134°.
) oraz podanie prawidłowego wyniku ∡𝐵𝑆𝐴 ≈ 134°.
2 pkt – poprawne wyprowadzenie i zapisanie związku 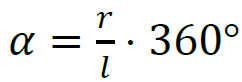 oraz zapisanie równania wynikającego z twierdzenia Pitagorasa dla trójkąta 𝐴𝑂𝑆: 𝑙2 = 𝑟2 + 𝐻2
oraz zapisanie równania wynikającego z twierdzenia Pitagorasa dla trójkąta 𝐴𝑂𝑆: 𝑙2 = 𝑟2 + 𝐻2
1 pkt – zapisanie równania 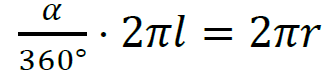
LUB
– zapisanie równania 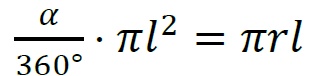
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.