Odpowiedź:
Przykładowe pełne rozwiązania
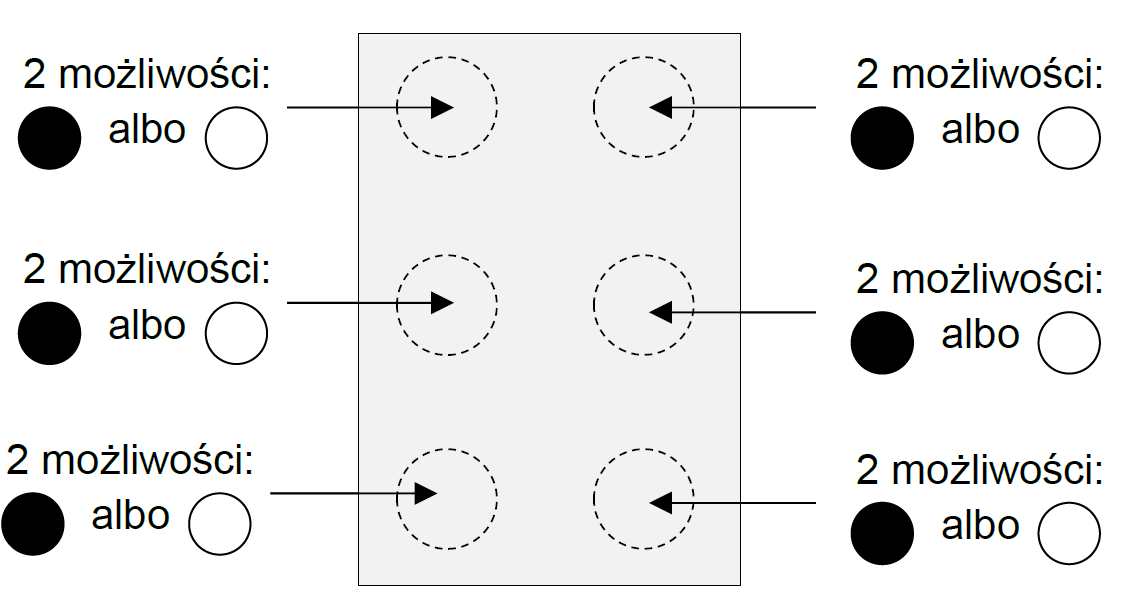





Sposób 1. (zastosowanie zasady mnożenia)
Zastosujemy regułę mnożenia. Zauważmy, że utworzenie znaku polega na podjęciu kolejno 6 decyzji o tym, jaki ma być rodzaj punktu – elementu znaku. Punkt może być wypukły albo może nie być wypukły. Zatem mamy dwie możliwości wyboru rodzaju punktu:

Zgodnie z regułą mnożenia, w takich przypadkach liczbę możliwości wyboru
składnika/elementu obiektu mnożymy przez siebie tyle razy, z ilu elementów składa się obiekt:
2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 64
Wszystkich możliwości (łącznie z utworzeniem konfiguracji 6 braków wypukłości) jest 64. Ponieważ znak Braille’a musi zawierać co najmniej jeden punkt wypukły, to wszystkich znaków jest:
64 − 1 = 63
Sposób 2. (bezpośrednie zliczenie liczby znaków z zastosowaniem zasady dodawania)
Będziemy kolejno zliczać „na piechotę” znaki: z jednym punktem wypukłym, z dwoma punktami wypukłymi, z trzema punktami wypukłymi, z czterema punktami wypukłymi, z pięcioma punktami wypukłymi i z sześcioma punktami wypukłymi. Zbiory znaków z daną liczbą punktów wypukłych oznaczymy odpowiednio jako: 𝐴1, 𝐴2, 𝐴3, 𝐴4, 𝐴5, 𝐴6.
Aby zliczanie przeprowadzić metodycznie, ułatwimy sobie zadanie numerując punkty w polu znaku, jak na rysunku obok.

W takiej konwencji, przykładowo:

𝐴1 = {(1), (2), (3), (4), (5), (6)}
|𝐴1| = 6

|𝐴2| = 15

|𝐴3| = 20
Zauważmy, że każdemu znakowi z dwoma punktami wypukłymi możemy przyporządkować znak z czterema punktami wypukłymi, zamieniając punkty wypukłe na niewypukłe i odwrotnie:

Zatem znaków z czterema punktami wypukłymi jest tyle samo, co znaków z dwoma punktami wypukłymi. Podobnie argumentujemy, że znaków z pięcioma punktami wypukłymi jest tyle samo co znaków z jednym punktem wypukłym:
|𝐴4| = |𝐴2| = 15 |𝐴5| = |𝐴1| = 6
𝐴6 = {(1,2,3,4,5,6)}
|𝐴6| = 1
Wszystkich znaków w piśmie Braille’a jest:
|𝐴1| + |𝐴2| + |𝐴3| + |𝐴4| + |𝐴5| + |𝐴6| = 6 + 15 + 20 + 15 + 6 + 1 = 63
schemat punktacji
2 pkt – zastosowanie prawidłowej metody do obliczenia wszystkich znaków, uwzględnienie warunku zadania i podanie wyniku: 63.
1 pkt – zapisanie wzoru na liczbę wszystkich możliwych znaków bez uwzględnienia warunku zadania (tzn. łącznie ze znakiem bez punktu wypukłego): 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2
LUB
– zastosowanie metody dodawania polegającej na bezpośrednim zliczeniu i dodaniu liczby znaków: z jednym punktem wypukłym, z dwoma punktami wypukłymi, z trzema punktami wypukłymi, z czterema punktami wypukłymi, z pięcioma punktami wypukłymi i z sześcioma punktami wypukłymi oraz prawidłowe zliczenie znaków w co najmniej trzech spośród sześciu wymienionych grup.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.