Odpowiedź:
Przykładowe pełne rozwiązania
Zbiór zdarzeń elementarnych Ω składa się ze wszystkich czterocyfrowych całkowitych liczb dodatnich.

Sposób 1. obliczenia mocy zbioru Ω.
Na diagramie poniżej rozpiszemy schemat liczby czterocyfrowej, gdzie dla każdej pozycji w zapisie dziesiętnym określimy, ile jest możliwości jej uzupełnienia.


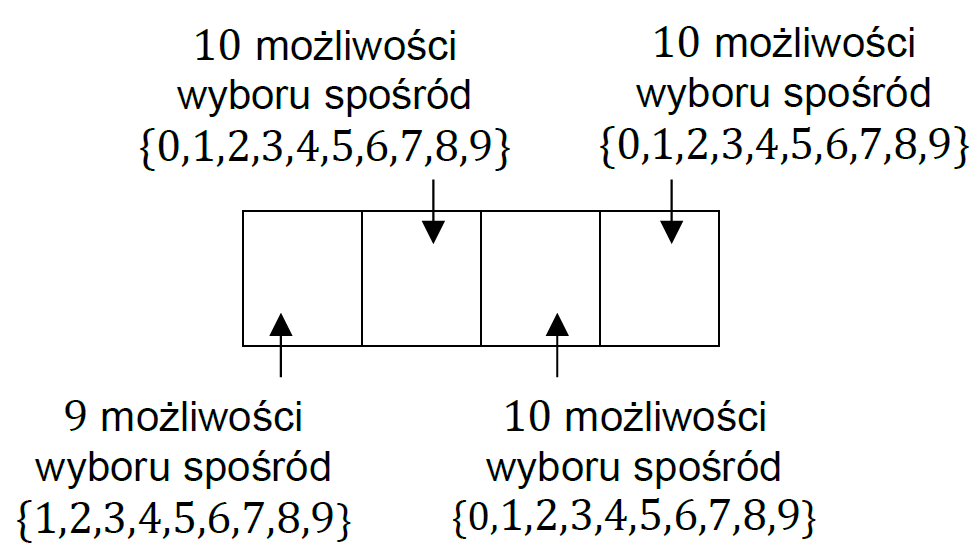
Zgodnie z zasadą mnożenia, wszystkich liczb czterocyfrowych dodatnich jest:

|Ω| = 9 ⋅ 10 ⋅ 10 ⋅ 10 = 9 000

Sposób 2. obliczenia mocy zbioru Ω.
Wszystkich ciągów czterech cyfr (także z zerem na pierwszej pozycji)


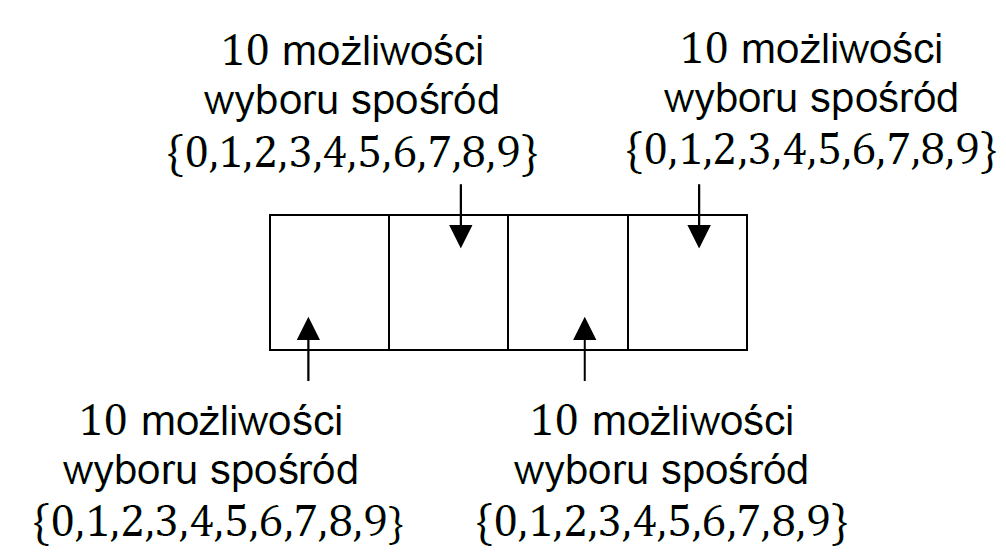
jest 10 ⋅ 10 ⋅ 10 ⋅ 10 = 10 000. Od tej liczby należy odjąć liczbę takich liczb, w których na pierwszej pozycji występuje zero – takich liczb jest 10 ⋅ 10 ⋅ 10 = 1000. Zatem wszystkich liczb czterocyfrowych dodatnich jest

|Ω| = 10 000 − 1 000 = 9 000.

(ciąg dalszy rozwiązania)
Określimy zdarzenie 𝐴 jako zbiór takich czterocyfrowych dodatnich liczb parzystych, w których zapisie dziesiętnym występują dokładnie jedna cyfra 2 i dokładnie jedna cyfra 3. Na poniższych diagramach z pozycjami cyfr rozpiszemy schematy liczb czterocyfrowych, spełniających te warunki.

• Liczby parzyste, które mają cyfrę 2 na pozycji czwartej oraz cyfrę 3 na pozycjach trzeciej, drugiej i pierwszej:




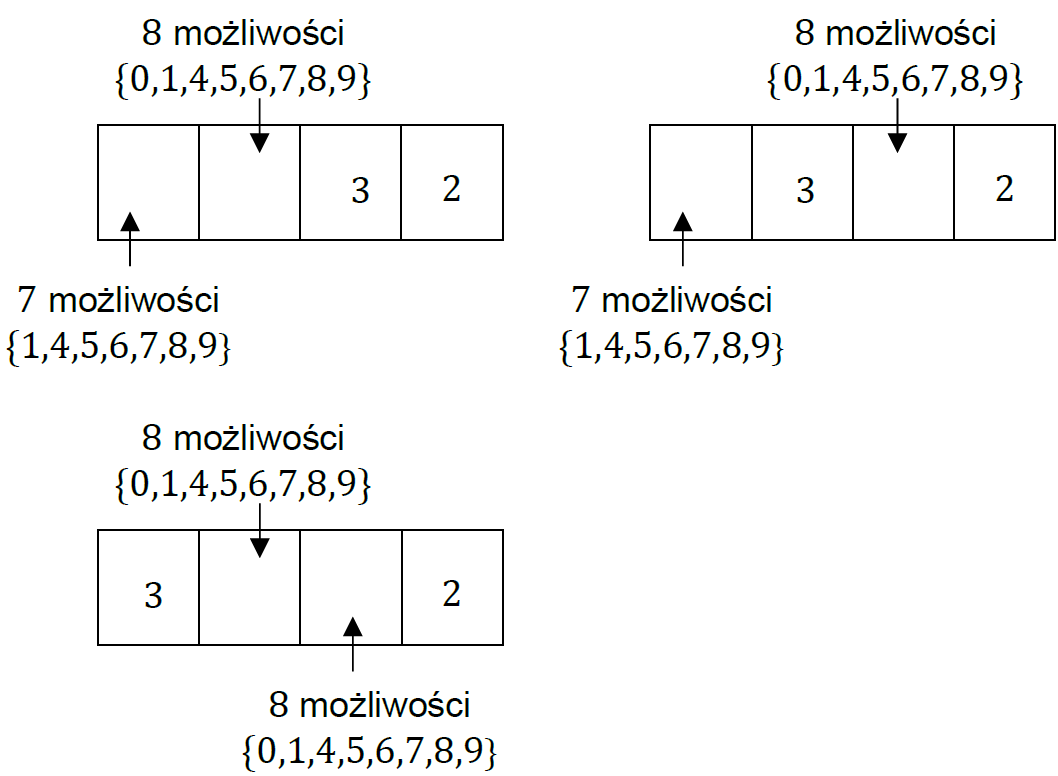
• Liczby parzyste, które na ostatniej pozycji mają cyfrę parzystą różną od cyfry 2 oraz cyfry 2 i 3 (dokładnie po jednej) na różnych pozycjach od pierwszej do trzeciej:



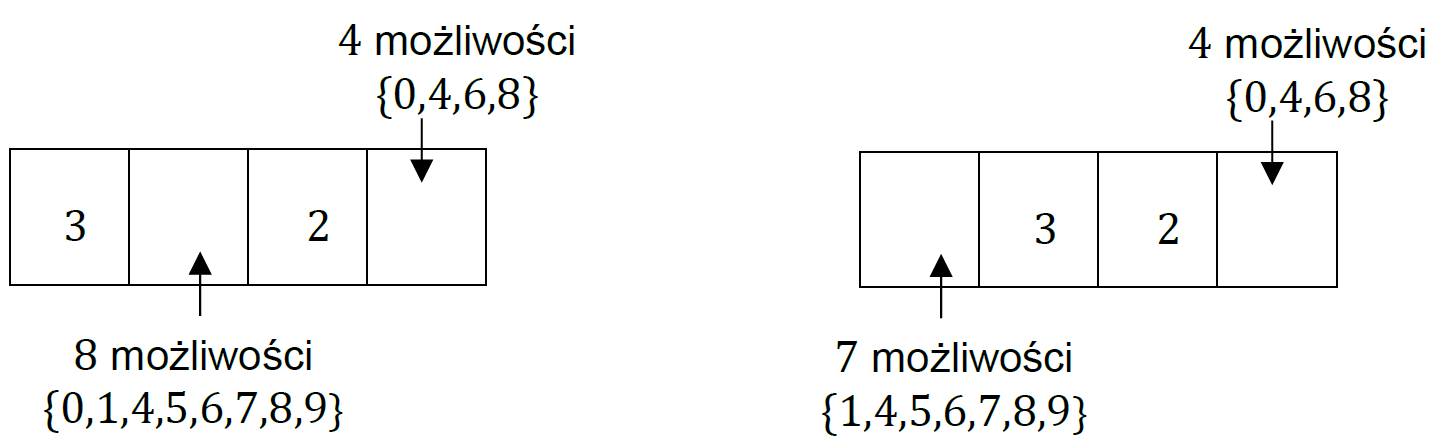
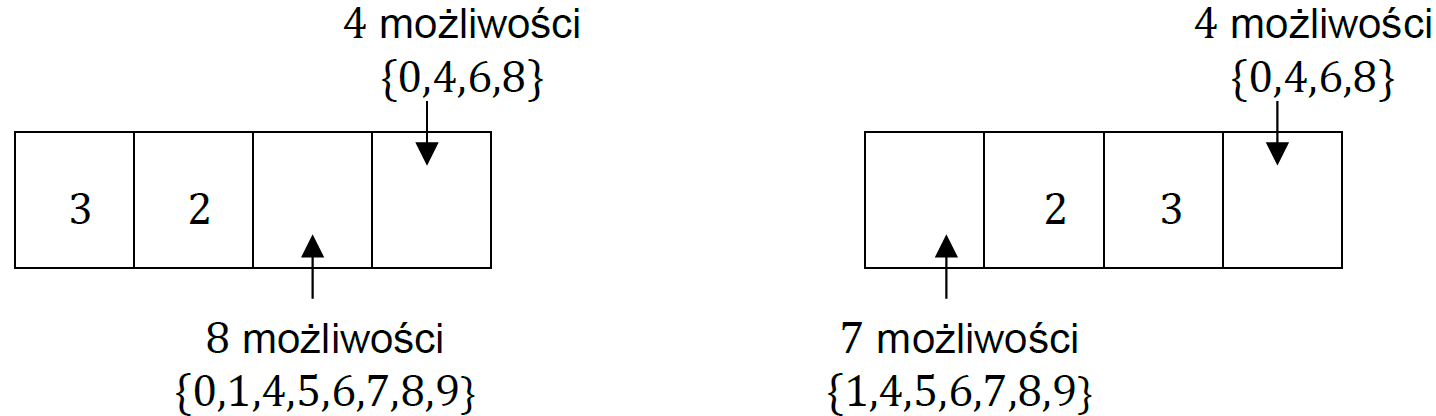
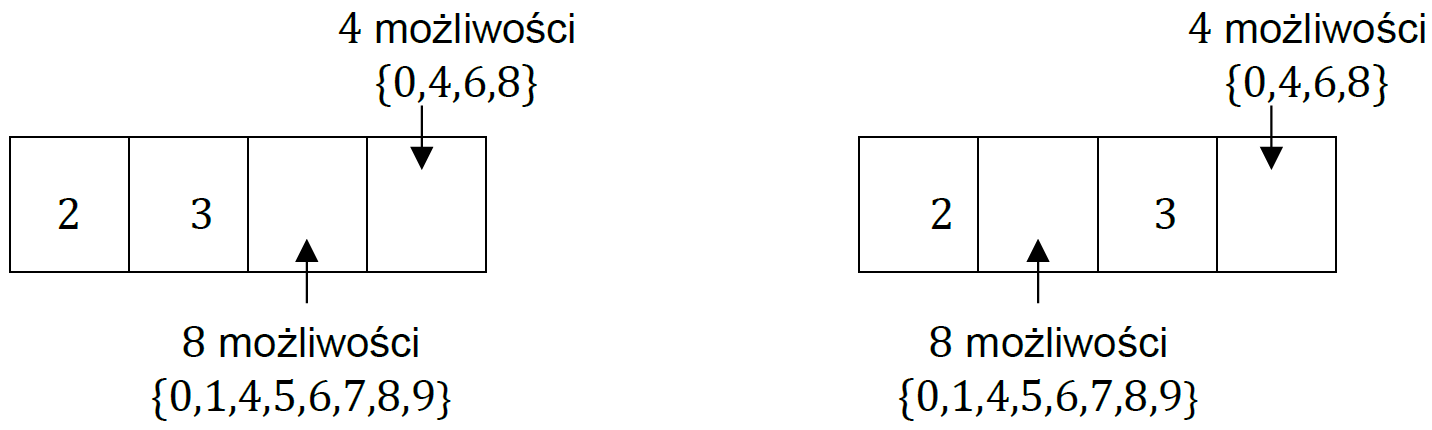
Liczbę zdarzeń elementarnych sprzyjających 𝐴 obliczymy z wykorzystaniem reguły mnożenia i dodawania łącznie:

|𝐴| = 7 ⋅ 8 + 7 ⋅ 8 + 8 ⋅ 8 + 8 ⋅ 4 + 7 ⋅ 4 + 8 ⋅ 4 + 7 ⋅ 4 + 8 ⋅ 4 + 8 ⋅ 4 = 360

Obliczymy prawdopodobieństwo zdarzenia 𝐴:




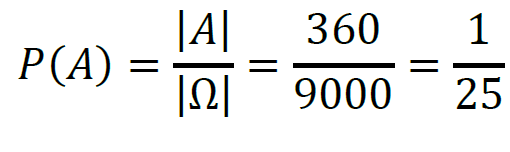
schemat punktacji
4 pkt – poprawna metoda obliczenia prawdopodobieństwa wylosowania czterocyfrowej, dodatniej liczby parzystej, w której zapisie dziesiętnym wystąpią dokładnie jedna cyfra 2 i dokładnie jedna cyfra 3, oraz podanie wyniku: 𝑃(𝐴) = 1⁄25

3 pkt – poprawna metoda obliczenia, ile jest wszystkich całkowitych liczb czterocyfrowych dodatnich oraz ile pośród nich jest liczb parzystych, w których zapisie dziesiętnym występują dokładnie jedna cyfra 2 i dokładnie jedna cyfra 3 oraz podanie prawidłowych wyników: |Ω| = 9 000, |𝐴| = 360
LUB
– zapisanie  oraz prawidłowa metoda obliczenia |𝐴|– ile jest dodatnich liczb parzystych, w których zapisie dziesiętnym występują dokładnie jedna cyfra 2 i dokładnie jedna cyfra 3, z błędem rachunkowym w obliczeniach.

2 pkt – poprawna metoda obliczenia, ile jest czterocyfrowych, dodatnich liczb parzystych, w których zapisie dziesiętnym występują dokładnie jedna cyfra 2 i dokładnie jedna cyfra 3, oraz podanie poprawnego wyniku: |𝐴| = 360
LUB
– poprawna metoda obliczenia, ile jest czterocyfrowych, dodatnich liczb parzystych, w których zapisie dziesiętnym występują dokładnie jedna cyfra 2 i dokładnie jedna cyfra 3, błąd rachunkowy w obliczeniach oraz poprawna metoda obliczenia, ile jest wszystkich całkowitych liczb czterocyfrowych dodatnich, i zapisanie wyniku: |Ω| = 9 000

1 pkt – poprawna metoda obliczenia, ile jest wszystkich całkowitych liczb czterocyfrowych dodatnich, i zapisanie wyniku: |Ω| = 9 ⋅ 10 ⋅ 10 ⋅ 10 = 9 000
LUB
– rozpisanie zbioru zdarzeń sprzyjających z prawidłowo określonymi wszystkimi możliwymi pozycjami cyfr 2 i 3 oraz cyframi parzystymi na końcu
LUB
– poprawna metoda zliczenia czterocyfrowych liczb parzystych z ostatnią (i dokładnie jedną) cyfrą 2 oraz dokładnie jedną cyfrą 3 w zapisie, łącznie z podaniem wyniku: 176.
LUB
– poprawna metoda zliczenia czterocyfrowych liczb parzystych z ostatnią cyfrą parzystą różną od 2 oraz dokładnie jedną cyfrą 3 i dokładnie jedną cyfrą 2 w zapisie, łącznie z podaniem wyniku: 184.

0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.