Odpowiedź:
Przykładowe pełne rozwiązania
Uwaga! Zgodnie z konwencją, do obliczeń przyjmuje się, że strata to zysk ujemny.
Sposób 1.
Wyprowadzimy wyrażenie ze zmienną 𝑥 na wartość oczekiwaną zysku z gry Pawła oraz na wartość oczekiwaną zysku z gry Grzegorza. Zaczniemy od Pawła.
1. Określimy zdarzenia wraz z ich prawdopodobieństwami, dla których następuje wymiana żetonów w grze:
Ω – zbiór wszystkich zdarzeń elementarnych – wyników rzutu kostką do gry.
Ω = {1,2,3,4,5,6} zatem |Ω| = 6
𝐴 – zdarzenie polegające na tym, że wypadła liczba oczek mniejsza od 4.
𝐴 = {1,2,3} zatem |𝐴| = 3
czyli
𝑃(𝐴) = 3⁄6 = 1⁄2
𝐵 – zdarzenie polegające na tym, że wypadła liczba oczek równa 6.
𝐵 = {6} zatem |𝐵| = 1
czyli
𝑃(𝐵) = 1⁄6
𝐶 – zdarzenie polegające na tym, że wypadła liczba oczek równa 4 lub 5.
𝐶 = {4,5} zatem |𝐶| = 2
czyli
𝑃(𝐶) = 2⁄6
2. Zyski Pawła przy zajściu zdarzeń 𝐴, 𝐵, 𝐶 są następujące (zyski Pawła oznaczymy 𝑍𝑃):
𝑍𝑃 (𝐴) = +10 żetonów
𝑍𝑃 (𝐵) = −𝑥 żetonów
𝑍𝑃 (𝐶) = 0 żetonów
Prawdopodobieństwa osiągnięcia tych zysków są takie, jak prawdopodobieństwa zdarzeń, przy których te zyski zachodzą:
𝑃(𝑍𝑃 (𝐴)) = 𝑃(𝐴) = 1⁄2
𝑃(𝑍𝑃 (𝐵)) = 𝑃(𝐵) = 1⁄6
𝑃(𝑍𝑃 (𝐶)) = 𝑃(𝐶) = 2⁄6
3. Obliczymy wartość oczekiwaną zysku z gry Pawła. Skorzystamy ze wzoru na wartość oczekiwaną:
𝔼𝑍𝑃 = 𝑍𝑃 (𝐴) ⋅ 𝑃(𝑍𝑃 (𝐴)) + 𝑍𝑃 (𝐵) ⋅ 𝑃(𝑍𝑃 (𝐵)) + 𝑍𝑃 (𝐶) ⋅ 𝑃(𝑍𝑃 (𝐶))
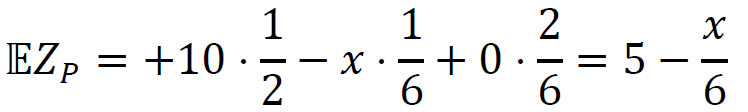
4. Analogicznie zapiszemy wyrażenie na wartość oczekiwaną zysku z gry Grzegorza. Zyski Grzegorza przy zajściu zdarzeń 𝐴, 𝐵, 𝐶 są następujące (zyski Grzegorza oznaczymy 𝑍𝐺 ):
𝑍𝐺 (𝐴) = −10 żetonów
𝑍𝐺 (𝐵) = +𝑥 żetonów
𝑍𝐺 (𝐶) = 0 żetonów
Zatem wartość oczekiwana zysku z gry Grzegorza dana jest wzorem:
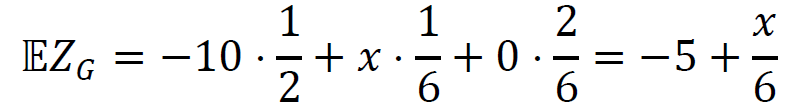
5. Zgodnie z warunkiem zadania, wartości oczekiwane zysku z gry Pawła i Grzegorza są sobie równe, zatem:
𝔼𝑍𝑃 = 𝔼𝑍𝐺
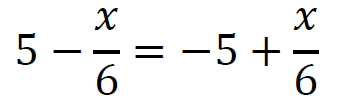
więc
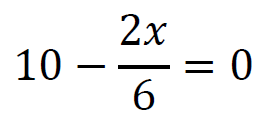
𝑥 = 30 żetonów
Sposób 2.
Wyprowadzimy wyrażenie ze zmienną 𝑥 na wartość oczekiwaną zysku Pawła.
Kroki 1.–3. są takie same jak w rozwiązaniu sposobem 1.
4. Zauważmy, że ta gra ma następującą szczególną własność: zysk jednego gracza jest stratą dla drugiego gracza. To oznacza, że wartości oczekiwane zysków Pawła i Grzegorza muszą być liczbami przeciwnymi, a z warunków zadania wynika – że muszą być liczbami równymi sobie. To oznacza, że wartości oczekiwane zysków z gry każdego z graczy są równe 0:
𝔼𝑍𝑃 = 0
5 - x⁄6 = 0
𝑥 = 30 żetonów
Uwaga
Fakt, że wartości oczekiwane zysków obu graczy są równe, nie oznacza, że żaden z nich nie osiągnie realnie w rezultacie gry większego zysku. Gra jest losowa, więc może zaistnieć sytuacja, że podczas całej gry będą wypadały kolejno same szóstki i Grzegorz będzie zyskiwał zawsze po 30 żetonów. Równość wartości oczekiwanych oznacza – w rozumieniu potocznym – że żaden z graczy nie ma „statystycznej przewagi” w osiągnięciu większego zysku.
schemat punktacji
3 pkt – poprawna metoda obliczenia liczby 𝑥 żetonów oraz zapisanie wyniku: 𝑥 = 30 żetonów.
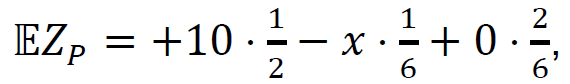
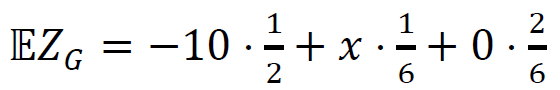
2 pkt – poprawne zapisanie wyrażenia na wartość oczekiwaną zysku Pawła oraz na wartość oczekiwaną zysku Grzegorza:
LUB
– poprawne zapisanie wyrażenia na wartość oczekiwaną zysku Pawła i stwierdzenie lub zapisanie, że jest ona równa zero, np.: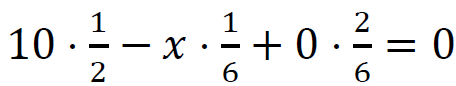
1 pkt – określenie i zapisanie prawdopodobieństw, z jakimi Paweł (lub Grzegorz) traci (lub zyskuje) liczbę 10 żetonów i liczbę 𝑥 żetonów (samo zapisanie prawdopodobieństw zdarzeń, bez powiązania zdarzeń z odpowiednim zyskiem lub stratą i bez dalszych obliczeń, nie spełnia tego kryterium).
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania