Odpowiedź:
Przykładowe pełne rozwiązanie
Rozwiązujemy układ (1) metodą podstawiania. Z pierwszego równania układu wyznaczamy 𝑦:

𝑦 = 𝑚2 − 𝑚𝑥

i wstawiamy do drugiego równania układu:

4𝑥 + 𝑚(𝑚2 − 𝑚𝑥) = 8

(4 − 𝑚2)𝑥 = 8 − 𝑚3

Zatem układ jest oznaczony, gdy 𝑚 ∈ ℝ\{−2 ; 2}. Wtedy



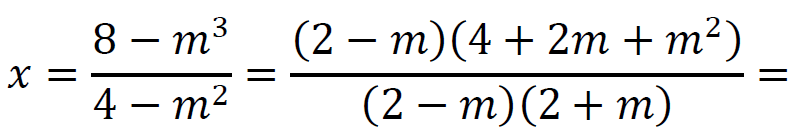
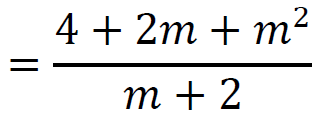
Stąd

𝑦 =
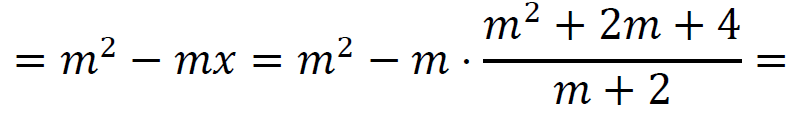
 1.7.png

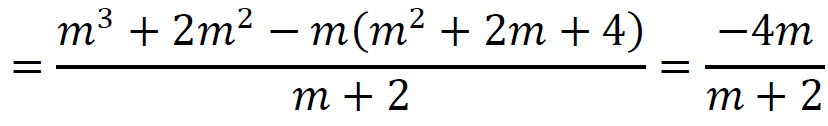
Wyznaczamy wartości parametru 𝑚, dla których prawdziwa jest nierówność |𝑥 + 𝑦| <  2:



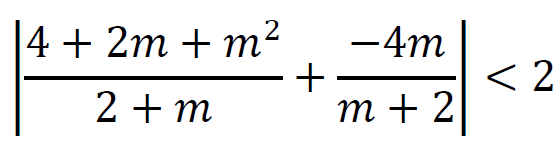
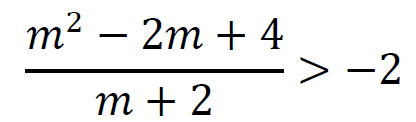1.11.png    i    

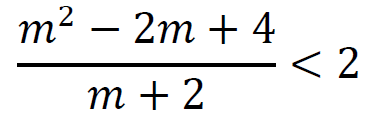
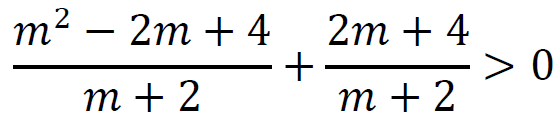
1.13.png    

                             i

   

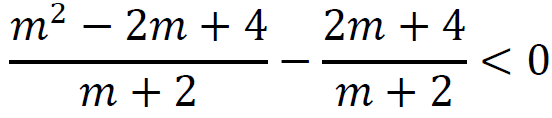
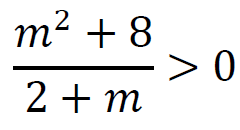1.15.png     i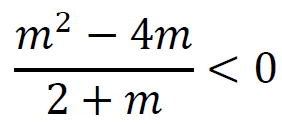   

(𝑚2 + 8)(𝑚 + 2) > 0 i 𝑚 ∈ ℝ\{−2 ; 2}    i     (𝑚2 − 4𝑚)(𝑚 + 2) < 0 i 𝑚 ∈ ℝ\{−2 ; 2}
𝑚 ∈ (−2 , 2) ∪ (2 , +∞)                           i     𝑚 ∈ (−∞ , −2) ∪ (0 , 2) ∪ (2 , 4)
co daje nam 𝑚 ∈ (0 , 2) ∪ (2 , 4).



schemat punktacji
6 pkt – poprawna metoda wyznaczenia wszystkich wartości parametru 𝑚 spełniających warunki zadania oraz prawidłowy wynik.

5 pkt – rozwiązanie nierówności 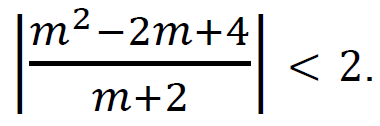1.1.png

4 pkt – rozwiązanie jednej z nierówności 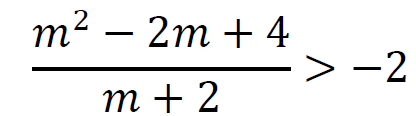1.3.png lub 

3 pkt – zapisanie nierówności 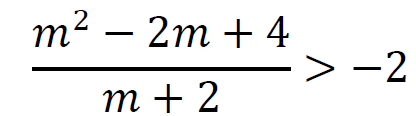1.3.png i 

2 pkt – wyznaczenie z układu (1) 𝑥 oraz 𝑦.

1 pkt – określenie wartości parametru 𝑚, dla jakich układ jest oznaczony i wyznaczenie z układu (1) 𝑥 lub 𝑦.

0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.