Odpowiedź:
Przykładowe pełne rozwiązanie
Skorzystamy z twierdzenia o pierwiastkach wymiernych wielomianu o współczynnikach całkowitych.
Na mocy tego twierdzenia wnosimy, że jeśli wielomian 𝑊 ma pierwiastek wymierny, to należy on do zbioru
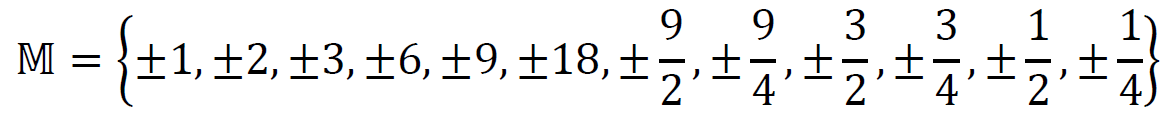
Na podstawie fragmentu wykresu funkcji 𝑊 stwierdzamy, że jeden z pierwiastków wielomianu znajduje się w przedziale (3⁄5 , 4⁄5). Tylko jedna liczba ze zbioru 𝕄 leży w tym przedziale i jest to ułamek 3⁄4.
Sprawdzamy, czy liczba 3⁄4 jest pierwiastkiem wielomianu 𝑊:
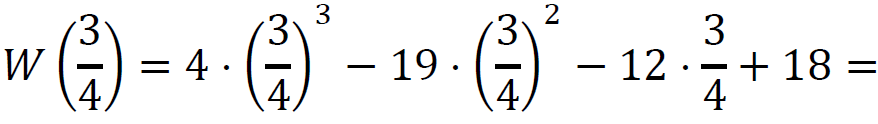
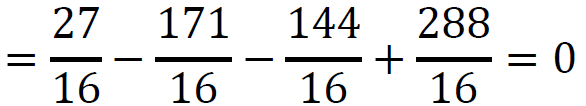
Zatem wielomian jest podzielny przez dwumian (𝑥 − 3⁄4).
Dzielimy wielomian 𝑊 przez dwumian (𝑥 − 3⁄4) i zapisujemy go w postaci iloczynowej:
𝑊(𝑥) = (𝑥 − 3⁄4)(4𝑥2 − 16𝑥 − 24).
Pierwiastkami trójmianu 4𝑥2 − 16𝑥 − 24 są liczby: 2 − √10 oraz 2 +√ 10.
Pierwiastkami wielomianu 𝑊 są liczby: 2 − √10 , 2 +√ 10, 3⁄4 .
schemat punktacji
3 pkt – obliczenie wszystkich pierwiastków wielomianu 𝑊.
2 pkt – sprawdzenie, że liczba 3⁄4 jest pierwiastkiem wielomianu oraz podzielenie wielomianu 𝑊 przez dwumian (𝑥 − 3⁄4).
1 pkt – zastosowanie twierdzenia o pierwiastkach wymiernych wielomianu i określenie liczb wymiernych mogących być pierwiastkami wielomianu 𝑊.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.