Odpowiedź:
Przykładowe pełne rozwiązanie
Funkcję 𝑓 przedstawiamy w postaci:
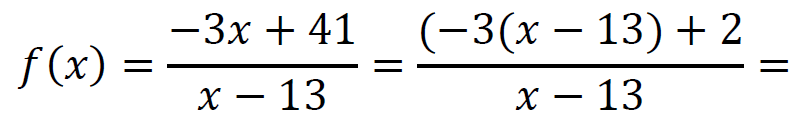
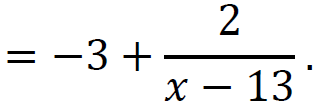
Wyznaczamy punkty kratowe.
Wartość funkcji będzie liczbą całkowitą tylko wtedy, gdy 2 ⁄ x - 13 ∈ ℤ. Szukamy całkowitych wartości 𝑥 (rożnych od 13) takich, dla których (𝑥 − 13) jest dzielnikiem 2. To prowadzi do następujących czterech przypadków:
• 𝑥 − 13 = −2, co daje 𝑥 = 11 i 𝑓(𝑥) = − 3 − 1 = −4 ∈ ℤ
• 𝑥 − 13 = −1, co daje 𝑥 = 12 i 𝑓(𝑥) = − 3 − 2 = −5 ∈ ℤ
• 𝑥 − 13 = 1, co daje 𝑥 = 14 i 𝑓(𝑥) = − 3 + 2 = −1 ∈ ℤ
• 𝑥 − 13 = 2, co daje 𝑥 = 15 i 𝑓(𝑥) = − 3 + 1 = −2 ∈ ℤ.
Do wykresu funkcji 𝑓 należą cztery punkty kratowe o współrzędnych: (11 , −4), (12 ,−5), (14 ,−1), (15 ,−2).
schemat punktacji
3 pkt – prawidłowe określenie wszystkich czterech możliwych przypadków, dla których 2 ⁄ x - 13 ∈ ℤ i prawidłowe wyznaczenie czterech punktów kratowych.
2 pkt – prawidłowe określenie dwóch z czterech możliwych przypadków, dla których 2 ⁄ x - 13 ∈ ℤ i prawidłowe wyznaczenie dwóch punktów kratowych.
1 pkt – przekształcenie postaci ogólnej funkcji homograficznej do postaci kanonicznej.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.