Odpowiedź:
Przykładowe pełne rozwiązanie
Wyznaczamy warunki konieczne i dostateczne na to, aby funkcja 𝑓 miała dokładnie dwa miejsca zerowe różniące się o jeden:
W1. 𝑝 ≠ 0 (z treści zadania 𝑓 jest funkcją kwadratową)
W2. Δ > 0 (aby funkcja 𝑓 miała dokładnie dwa miejsca zerowe)
W3. |𝑥1 − 𝑥2| = 1 (aby miejsca zerowe funkcji 𝑓 różniły się o 1).
Rozwiązujemy warunek W2:
Δ > 0
(𝑝 − 1)2 − 4𝑝(1 − 2𝑝) > 0
9𝑝2 − 6𝑝 + 1 > 0
(3𝑝 − 1)2 > 0
𝑝 ∈ (−∞ , 1⁄3) ∪ (1⁄3 , +∞)
Rozwiązujemy warunek W3. Skorzystamy tutaj ze wzorów Viète’a.
|𝑥1 − 𝑥2| = 1
(𝑥1 − 𝑥2)2 = 1
(𝑥1 + 𝑥2)2 −4 𝑥1 ⋅ 𝑥2 = 1
Gdy 𝑝 ≠ 0 mamy
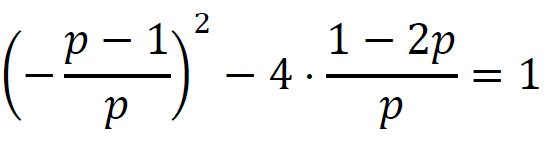
(𝑝 − 1)2 − 4𝑝(1 − 2𝑝) = 𝑝2
8𝑝2 − 6𝑝 + 1 = 0
𝑝 = 1⁄2 lub 𝑝 = 1⁄4
Po uwzględnieniu wszystkich warunków otrzymujemy: 𝑝 = 1⁄2 lub 𝑝 = 1⁄4 .
schemat punktacji
4 pkt – zapisanie zbioru tych wszystkich wartości parametru 𝑝, dla których funkcja ma dokładnie dwa miejsca zerowe różniące się o 1 .
3 pkt – zapisanie nierówności Δ > 0 w zależności od parametru 𝑝 i jej rozwiązanie oraz zapisanie warunku |𝑥1 − 𝑥2| = 1 w zależności od parametru 𝑝 i jego rozwiązanie.
2 pkt – zapisanie nierówności Δ > 0 w zależności od parametru 𝑝 i jej rozwiązanie
LUB
zapisanie warunku |𝑥1 − 𝑥2| = 1 w zależności od parametru 𝑝 i jego rozwiązanie.
1 pkt – wyznaczenie warunków koniecznych i dostatecznych na to, aby funkcja 𝑓 miała dokładnie dwa miejsca zerowe różniące się o 1.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.