Odpowiedź:
Przykładowe pełne rozwiązania
Sposób 1. (z wykorzystaniem definicji).
Niech 𝑥1 , 𝑥2 ∈ (−1 , +∞) oraz 𝑥2 > 𝑥1. Wtedy


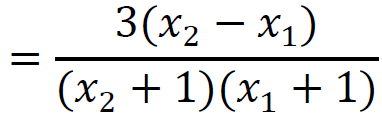
Dla 𝑥2 > 𝑥1 różnica 𝑥2 − 𝑥1 jest dodatnia, ponadto dla 𝑥1 , 𝑥2 ∈ (−1 , +∞) każda z sum
(𝑥2 + 1) oraz (𝑥1 + 1) jest dodatnia, więc iloraz 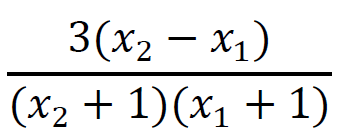 również jest dodatni.
również jest dodatni.
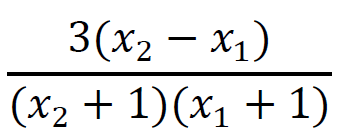 również jest dodatni.
również jest dodatni.Oznacza to, że 𝑓(𝑥2) > 𝑓(𝑥1) dla 𝑥1 , 𝑥2 ∈ (−1 , +∞) oraz 𝑥2 > 𝑥1, zatem funkcja 𝑓 jest rosnąca w przedziale (−1 , +∞).
To kończy dowód.
Sposób 2. (z wykorzystaniem rachunku różniczkowego).
Niech 𝑥 ∈ (−1 , +∞). Obliczamy pochodną 𝑓′ funkcji 𝑓:

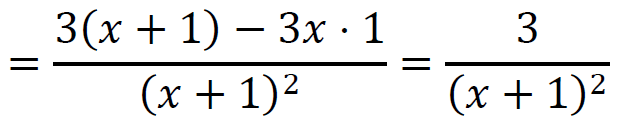
dla każdego 𝑥 ∈ (−1 , +∞).
Funkcja 𝑓 jest różniczkowalna w przedziale (−1 , +∞), a jej pochodna jest w każdym punkcie tego przedziału dodatnia. Zatem funkcja 𝑓 jest w tym przedziale rosnąca.
To kończy dowód.
Sposób 3. (oparty na definicji funkcji rosnącej).
Niech 𝑥1 , 𝑥2 ∈ (−1 , +∞) będą dwoma dowolnymi argumentami funkcji 𝑓. Załóżmy, że 𝑥1 < 𝑥2. Wtedy
0 < 𝑥1 + 1 < 𝑥2 + 1
Dzieląc obie strony tej nierówności przez liczbę dodatnią (𝑥1 + 1)(𝑥2 + 1), otrzymujemy nierówność równoważną

i dalej

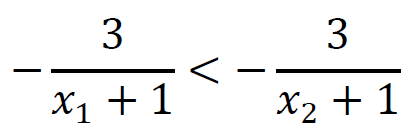
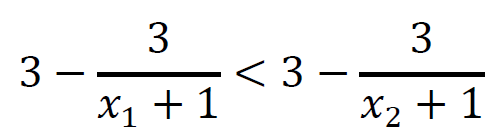
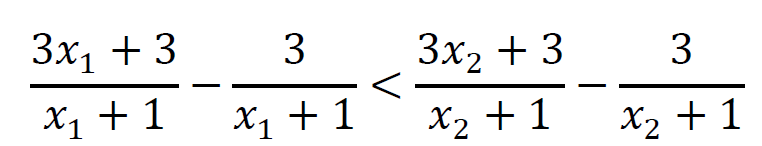
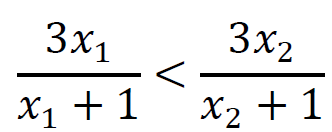
𝑓(𝑥1) < 𝑓(𝑥2)
To oznacza, że funkcja 𝑓 jest rosnąca.
Sposób 4. (z wykorzystaniem własności funkcji postaci 𝑦 = a⁄x ).
Wzór funkcji 𝑓 przedstawiamy w postaci:
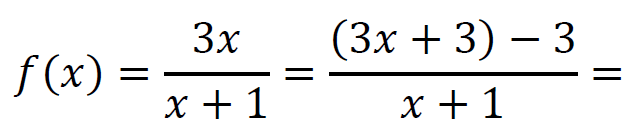

Wykres funkcji 𝑓 można uzyskać przez przesunięcie wykresu funkcji 𝑔(𝑥) = − 3⁄x (określonej dla 𝑥 > 0) o wektor [−1 , 3]. Z wykresu/własności funkcji 𝑔 wynika, że funkcja 𝑔 jest rosnąca dla 𝑥 > 0, więc funkcja 𝑓 jest rosnąca dla 𝑥 > −1.
To kończy dowód.
Sposób 5. (oparty na umiejętności porównywania ułamków).
Wzór funkcji 𝑓 przedstawiamy w postaci:
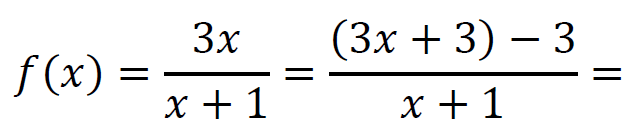

Dla każdej liczby rzeczywistej 𝑥 > −1 ułamek 3⁄ x + 1 jest dodatni, a ponieważ licznik jest stały i dodatni, to ułamek jest tym mniejszy, im jego mianownik jest większy. Zatem ze wzrostem liczby 𝑥 > −1 liczba 3 − 3⁄ x + 1 jest coraz większa. Tym samym funkcja 𝑓 jest rosnąca.
schemat punktacji
dla rozwiązań sposobami 1., 2. oraz 3.
3 pkt – przeprowadzenie pełnego dowodu.
2 pkt – poprawne określenie znaku różnicy
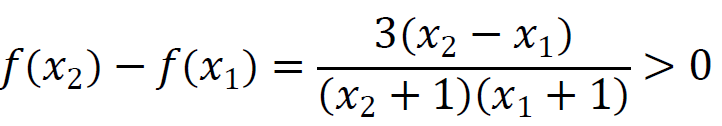
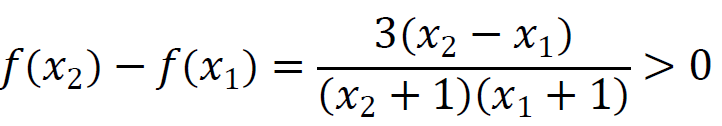
LUB
pochodnej 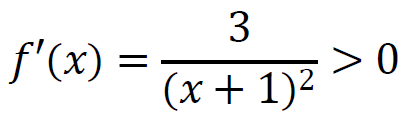
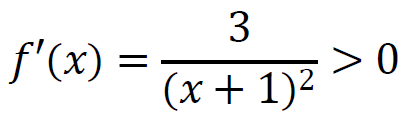
LUB
przekształcenie nierówności 𝑥2 > 𝑥1 do postaci 
1 pkt – przyjęcie założeń 𝑥1 , 𝑥2 ∈ (−1 ; +∞) i 𝑥2 > 𝑥1 oraz obliczenie różnicy 
LUB
przyjęcie założenia 𝑥 ∈ (−1 ; +∞) oraz obliczenie pochodnej 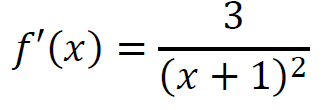
LUB
przyjęcie założeń 𝑥1 , 𝑥2 ∈ (−1 ; +∞) i 𝑥2 > 𝑥1 oraz przekształcenie nierówności 𝑥2 > 𝑥1 do postaci 
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.
dla rozwiązań sposobami 4. oraz 5.
3 pkt – przeprowadzenie pełnego dowodu.
2 pkt – zapisanie, że wykres funkcji 𝑓 można otrzymać z przesunięcia wykresu funkcji 𝑔(𝑥) = − 3⁄x o wektor [−1,3]
LUB
uzasadnienie, że wraz ze wzrostem liczby 𝑥 > −1 wartość ułamka 3⁄ x + 1 zmniejsza się.
1 pkt – zapisanie funkcji 𝑓 w postaci 𝑓(𝑥) = 3 − 3⁄ x + 1 .
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.