Odpowiedź:
Przykładowe pełne rozwiązanie
Najpierw wyznaczymy najmniejszą odległość, na jaką Syzyf zbliży się do wierzchołka góry.
Obliczamy pochodną funkcji 𝑥:
𝑥′(𝑡) = −3𝑡2 + 33𝑡 + 180 dla 𝑡 ∈ [0 , 24]
i obliczamy jej miejsca zerowe: 𝑥′(𝑡) = 0
−3𝑡2 + 33𝑡 + 180 = 0
𝑡2 − 11𝑡 − 60 = 0
Δ = 361
𝑡1 = 15 𝑡2 < 0
Ponieważ:
𝑥′(𝑡) > 0 dla 𝑡 ∈[ 0 , 15)
𝑥′(𝑡) < 0 dla 𝑡 ∈ (15 , 24]
więc
funkcja 𝑥 jest rosnąca w przedziale [0 , 15]
funkcja 𝑥 jest malejąca w przedziale [15 , 24]
Zatem 𝑥𝑚𝑎𝑥= 𝑥(15) = 3037,5 i Syzyf zbliży się do wierzchołka góry na odległość 962,5 m.
Obliczamy maksymalną wartość prędkości, z jaką Syzyf wtacza kulę.
Niech v oznacza prędkość Syzyfa wtaczającego kulę.
Ponieważ v = 𝑥′ , więc
v(𝑡) = 𝑥′(𝑡) = −3𝑡2 + 33𝑡 + 180 dla 𝑡 ∈ [0 , 24]
Korzystamy z własności funkcji kwadratowej i obliczamy największą wartość prędkości, z jaką Syzyf wtacza kulę:
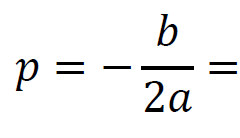
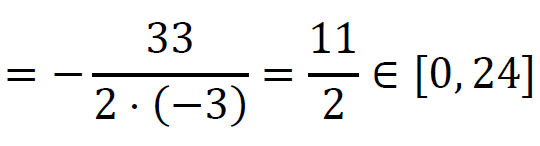
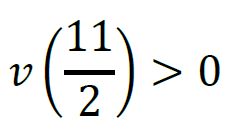
Zatem największa wartość prędkości, z jaką Syzyf wtacza kulę pod górę jest równa
v(5,5) = 270,75 m/h.
schemat punktacji
4 pkt – poprawna metoda wyznaczenia najmniejszej odległości, na jaką Syzyf zbliży się do wierzchołka góry, i poprawna metoda wyznaczenia największej wartości prędkości, z jaką wtaczany jest kamień, wraz z prawidłowymi wynikami liczbowymi.
3 pkt – zapisanie, że prędkość jest pochodną funkcji położenia i znalezienie ekstremów funkcji 𝑥′.
2 pkt – zbadanie monotoniczności funkcji 𝑥 i znalezienie ekstremów funkcji 𝑥.
1 pkt – obliczenie pochodnej funkcji 𝑥.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.