Odpowiedź:
Przykładowe pełne rozwiązanie
Rozpatrzmy sieć dróg złożoną z odcinków 𝐴𝐾, 𝐾𝐿, 𝐿𝐶, 𝐵𝐿 i 𝐷𝐾 (zobacz rysunek 1.)

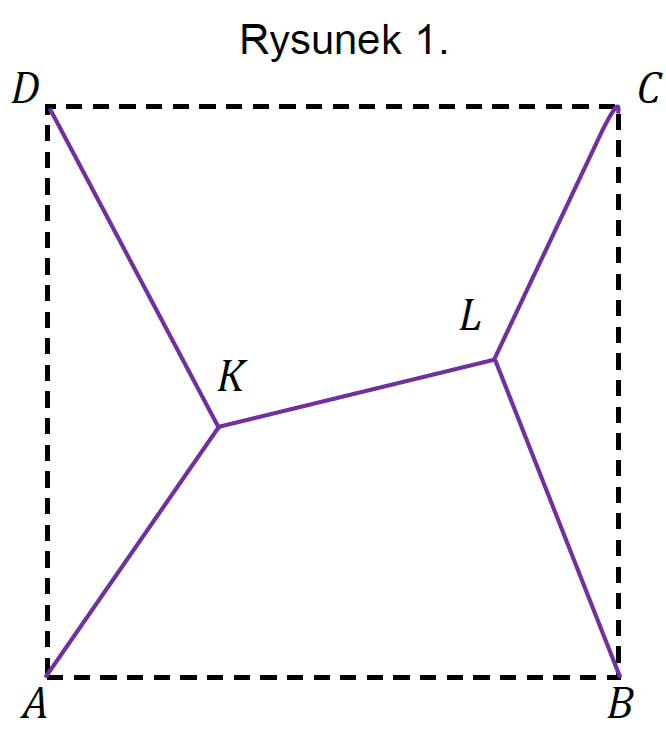
10.1.png

Prowadzimy prostą 𝑝 równoległą do 𝐴𝐷 i przechodzącą przez 𝐾 i zaznaczamy na niej punkt 𝐾’ taki, że |𝐴𝐾′|=|𝐷𝐾′|.

Prowadzimy prostą równoległą do 𝐵𝐶 i przechodzącą przez 𝐿 i zaznaczamy na niej punkt 𝐿’ taki, że |𝐵𝐿′|=|𝐶𝐿′| (patrz rysunek 2.).


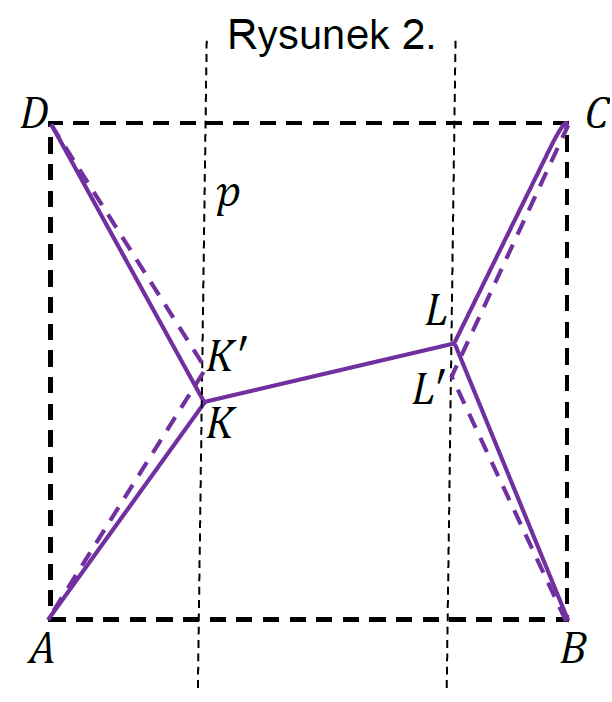
Pokażemy, że sieć dróg z węzłami 𝐾 i 𝐿 można zastąpić siecią krótszą – z węzłami 𝐾’ i 𝐿’.
Niech 𝐷’ będzie punktem symetrycznym do punktu 𝐷 względem prostej 𝑝. Wówczas punkty 𝐷’, 𝐾’ oraz 𝐴 są współliniowe, więc

|𝐷𝐾| + |𝐾𝐴| = |𝐷′𝐾| + |𝐾𝐴| ≥ |𝐷′𝐴| = |𝐷𝐾′| + |𝐾′𝐴|.

Podobnie pokazujemy, że |𝐵𝐿| + |𝐿𝐶| ≥ |𝐵𝐿′| + |𝐿′𝐶|. Ponadto odcinek 𝐾′𝐿′ jest równoległy do prostej 𝐴𝐵, więc |𝐾′𝐿′| ≤ |𝐾𝐿|. Zatem sieć dróg z węzłami 𝐾′ i 𝐿′ jest krótsza niż z węzłami 𝐾 i 𝐿.
Oznaczmy odległość punktu 𝐾′ od prostej 𝐴𝐷 przez 𝑥, natomiast punktu 𝐿′ od prostej 𝐵𝐶 przez 𝑦. Długość 𝑑 sieci z węzłami 𝐾′ i 𝐿′ jest równa

 + 300 − 𝑥 − 𝑦

gdzie 𝑥 ∈ [0 , 300] i 0 ≤ 𝑥 + 𝑦 < 300.

Zbadamy funkcję 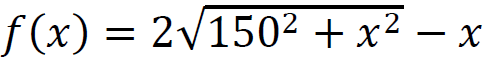f1.png określoną dla 𝑥 ∈ [0 , 300].



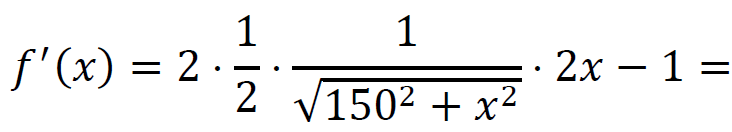
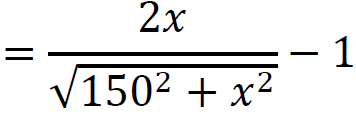
𝑓′(𝑥) = 0


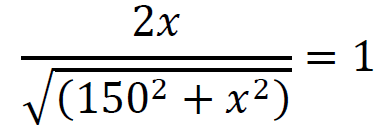
4𝑥2 = 𝑥2 + 1502

𝑥 = 50√3

𝑓′(𝑥) > 0 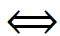wtiw.png 𝑥 ∈ (50√3 , 300]

𝑓′(𝑥) < 0 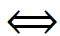wtiw.png  𝑥 ∈ [0 , 50√3)

Funkcja 𝑓 jest malejąca w przedziale [0 , 50√3] i rosnąca w przedziale [50√3 , 300]. Najmniejszą wartość funkcja przyjmuje w punkcie 𝑥 = 50√3 i wartość ta jest równa 𝑓(50√3) = 150√3.

Zatem

𝑑 = 𝑓(𝑥) + 𝑓(𝑦) + 300 ≥ 300(1 + √3)

przy czym równość zachodzi tylko wtedy, gdy 𝑥 = 𝑦 = 50√3. Najkrótsza sieć dróg ma zatem długość 300(1 + √3) km i składa się z 5 odcinków: 𝐴𝐾′, 𝐾′𝐿′, 𝐿′𝐶, 𝐵𝐿′ i 𝐷𝐾′.

Węzeł 𝐾′ jest równo oddalony (w odległości 100 √3 km) od miast 𝐴 i 𝐷, natomiast węzeł 𝐿′ jest równo oddalony (w odległości 100 √3 km) od miast 𝐵 i 𝐶 (patrz rysunek 2.).

Zauważmy jeszcze, że w przypadku sieci dróg z jednym węzłem, najkrótsza taka sieć będzie miała długość równą 600√3  km (i węzeł w środku kwadratu 𝐴𝐵𝐶𝐷). Będzie więc dłuższa niż sieć z dwoma węzłami.
schemat punktacji
6 pkt – obliczenie długości najkrótszej sieci z dwoma węzłami i podanie lokalizacji węzłów względem miast.
5 pkt – obliczenie długości najkrótszej sieci z dwoma węzłami.
4 pkt – obliczenie wartości najmniejszej funkcji 𝑓.
3 pkt – obliczenie pochodnej funkcji 𝑓.
2 pkt – wyrażenie długości sieci za pomocą odległości węzłów od prostych odpowiednio 𝐴𝐷 i 𝐵𝐶.
1 pkt – uzasadnienie, że węzły muszą się znajdować na symetralnej odcinka 𝐴𝐷.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.