Odpowiedź:
Przykładowe pełne rozwiązania
Sposób 1.
Wyznaczamy pochodną funkcji 𝑓 korzystając z twierdzenia o pochodnej funkcji złożonej:
𝑓′(𝑥) = 4𝑥3 + 0,5 ⋅ 4(2𝑥 + 1)3 ⋅ 2 dla 𝑥 ∈ ℝ .
Obliczamy miejsca zerowe pochodnej funkcji 𝑓:
4𝑥3 + 0,5 ⋅ 4(2𝑥 + 1)3 ⋅ 2 = 0
𝑥3 + (2𝑥 + 1)3 = 0
(𝑥 + 2𝑥 + 1)[𝑥2 − 𝑥(2𝑥 + 1) + (2𝑥 + 1)2 ] = 0
(3𝑥 + 1)(3𝑥2 + 3𝑥 + 1) = 0
3𝑥 + 1 = 0 lub 3𝑥2 + 3𝑥 + 1 = 0
Pierwsze z tych równań ma rozwiązanie 𝑥 = −1⁄3 , natomiast drugie jest sprzeczne.
Sprawdzamy, czy w punkcie 𝑥 = −1⁄3 funkcja 𝑓 osiąga ekstremum. Badamy monotoniczność funkcji 𝑓 stosując rachunek pochodnych:
𝑓′(𝑥) = 4𝑥3 + 0,5 ⋅ 4(2𝑥 + 1)3 ⋅ 2 = 4(3𝑥 + 1)(3𝑥2 + 3𝑥 + 1)
𝑓′(𝑥) > 0 dla 𝑥 ∈ (−1⁄3 ; +∞)
𝑓′(𝑥) < 0 dla 𝑥 ∈ (−∞ ; −1⁄3)
więc
funkcja 𝑓 jest malejąca w zbiorze (−∞ ; −1⁄3]
funkcja 𝑓 jest rosnąca w zbiorze [−1⁄3 ; +∞),
co oznacza, że w punkcie 𝑥 = −1⁄3 funkcja 𝑓 ma ekstremum lokalne, będące jednocześnie minimum globalnym. Funkcja 𝑓 osiąga wartość najmniejszą równą
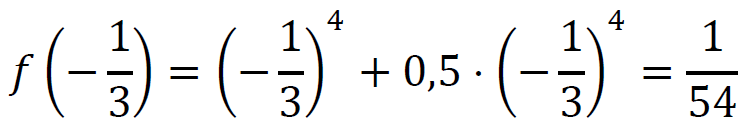
Sposób 2.
Korzystamy z nierówności między średnimi liczbowymi.
Dla każdych liczb nieujemnych 𝑎, 𝑏, 𝑐 średnia kwadratowa z tych liczb jest niemniejsza od średniej arytmetycznej tych liczb:
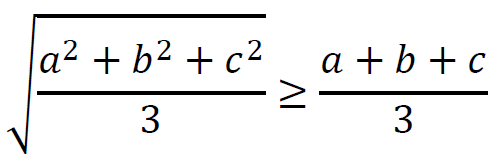
Niech 𝑥 będzie dowolną liczbą rzeczywistą. Korzystając z nierówności między średnią kwadratową a arytmetyczną liczb 𝑥2, 𝑥2, (2𝑥+1)2 otrzymujemy:
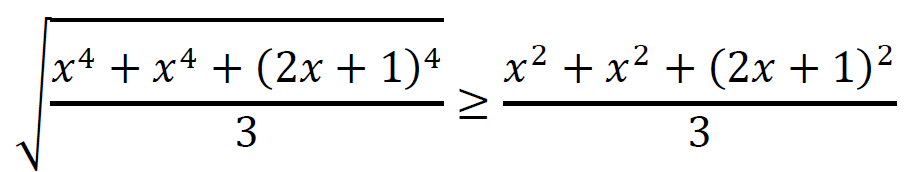
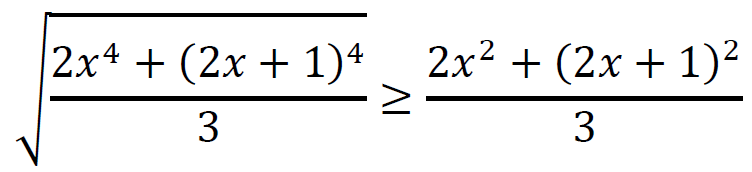
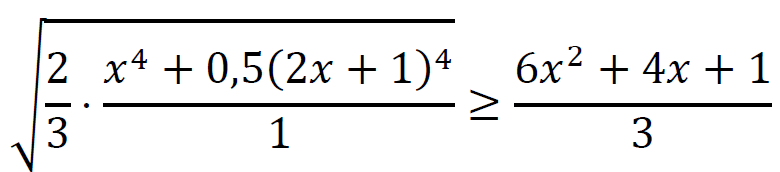
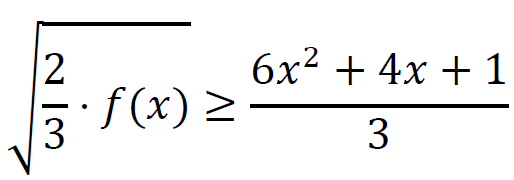
dla każdego 𝑥 ∈ ℝ.
Funkcja kwadratowa 𝑦 = 6𝑥2 + 4𝑥 + 1 osiąga wartość najmniejszą dla
równą 
więc
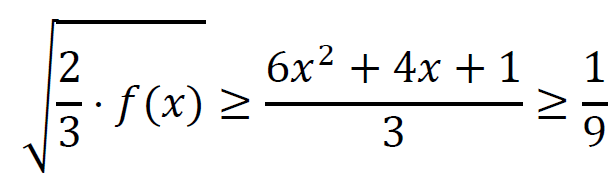
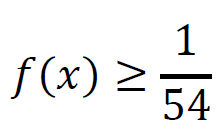
dla każdego 𝑥 ∈ ℝ.
Ponieważ
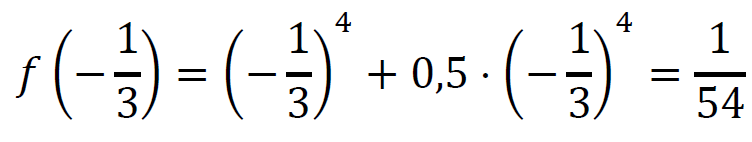
więc najmniejsza wartość funkcji 𝑓 jest równa 1⁄ 54 .
Sposób 3.
Niech 𝑡 = 𝑥 + 1⁄3 dla 𝑥 ∈ ℝ. Wtedy
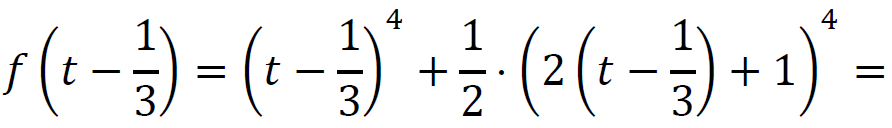
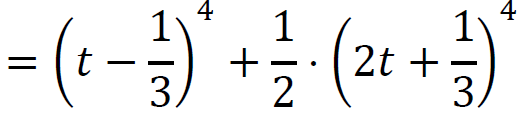dla 𝑡 ∈ ℝWykorzystamy dwukrotnie wzór na czwartą potęgę sumy dwóch składników
(𝑎 + 𝑏)4 = 𝑎4 + 4𝑎3𝑏 + 6𝑎2𝑏2 + 4𝑎𝑏3 + 𝑏4
Wówczas
𝑓(𝑡 − 1⁄3) = 𝑡 4 − 4𝑡3 ⋅ 1⁄3 + 6𝑡2 ⋅ 1⁄9 − 4𝑡 ⋅ 1⁄27 + 1⁄81 + 1⁄2 (16𝑡4 + 4 ⋅ 8𝑡3 ⋅ 1⁄3 + 6 ⋅ 4𝑡2 ⋅ 1⁄9 + 4 ⋅ 2𝑡 ⋅ 1⁄27 + 1⁄81 ) = 9𝑡4 + 4𝑡3 + 2𝑡2 + 1⁄ 54 = 9𝑡2 (𝑡2 + 4⁄9𝑡 + 2⁄9) + 1⁄ 54 = 9𝑡2((𝑡 + 2⁄9)2 + 14⁄81) + 1⁄ 54
Ponieważ dla każdego 𝑡 ∈ ℝ prawdziwe są nierówności:
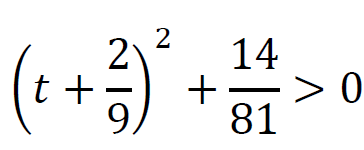
więc 𝑓(𝑡 − 1⁄3) ≥ 1⁄ 54 , przy czym 𝑓(𝑡 − 1⁄3) = 1⁄ 54 wtedy i tylko wtedy, gdy 𝑡 = 0 (czyli dla 𝑥 = − 1⁄3).
Zatem najmniejsza wartość funkcji 𝑓 jest równa 1⁄ 54.
schemat punktacji
dla rozwiązania sposobem 1.
4 pkt – obliczenie wartości najmniejszej funkcji 𝑓.
3 pkt – uzasadnienie (np. poprzez badanie monotoniczności funkcji), że funkcja 𝑓 przyjmuje wartość najmniejszą dla 𝑥 = −1⁄3.
2 pkt – obliczenie miejsc zerowych pochodnej funkcji 𝑓.
1 pkt – wyznaczenie pochodnej funkcji 𝑓.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.
dla rozwiązania sposobem 2.
4 pkt – obliczenie wartości najmniejszej funkcji 𝑓.
3 pkt – zapisanie, że funkcja kwadratowa 𝑦 = 6𝑥2 + 4𝑥 + 1 osiąga wartość najmniejszą równą 1⁄3 dla 𝑥 = −1⁄3.
2 pkt – zapisanie nierówności
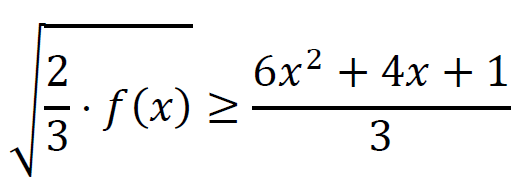
1 pkt – zapisanie nierówności
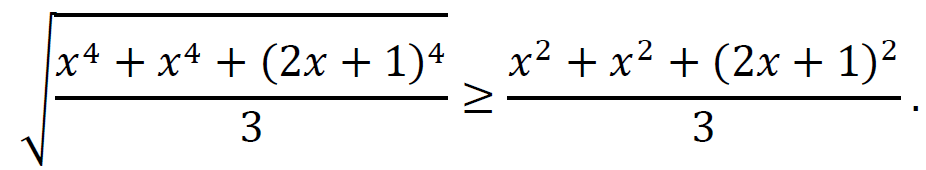
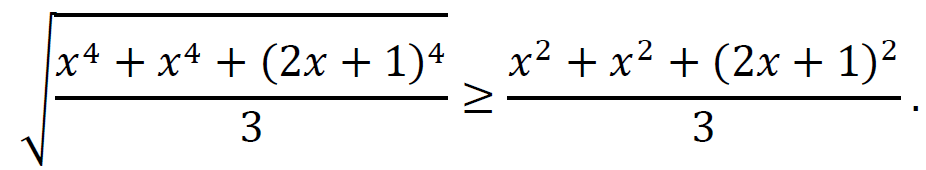
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.
dla rozwiązania sposobem 3.
4 pkt – obliczenie wartości najmniejszej funkcji 𝑓.
3 pkt – przekształcenie wyrażenia 9𝑡4 + 4𝑡3 + 2𝑡2 + 1⁄54 do postaci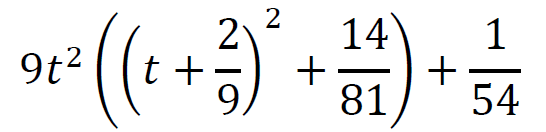 
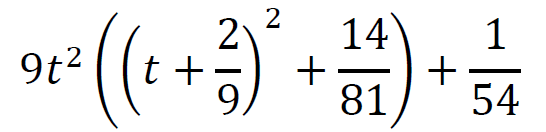
2 pkt – zastosowanie wzoru na czwartą potęgę sumy/różnicy dwóch wyrażeń i zapisanie funkcji 𝑓 jako
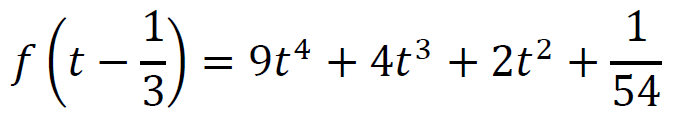
1 pkt – zastosowanie podstawienia 𝑡 = 𝑥 − 1⁄3 i zapisanie funkcji 𝑓 w postaci
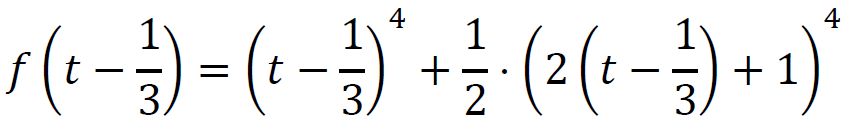
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.