Odpowiedź:
Przykładowe pełne rozwiązanie
Załóżmy, że układ równań (1)–(2) ma rozwiązanie w zbiorze liczb rzeczywistych nie mniejszych od 4. Wtedy
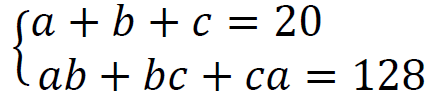
Przekształcamy układ równań do postaci, w której otrzymamy równanie kwadratowe z niewiadomą 𝑎 i parametrem 𝑐:
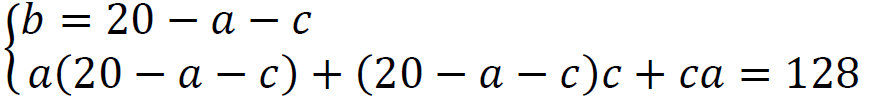
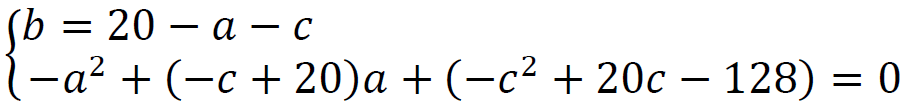
Równanie 𝑎2 + (𝑐 − 20)𝑎 + (𝑐2 − 20𝑐 + 128) = 0 ma z założenia rozwiązanie, więc wyróżnik Δ𝑎 jest nieujemny, co prowadzi do:
Δ𝑎 ≥ 0
(𝑐 − 20)2 − 4(𝑐2 − 20𝑐 + 128) ≥ 0
−3𝑐2 + 40𝑐 − 112 ≥ 0
−3(𝑐 − 4)(𝑐 − 28⁄3) ≥ 0
𝑐 ∈ [4 , 28⁄3]
Jeśli 𝑐 ∈ [4 , 28⁄3], to funkcja 𝑓(𝑎) = 𝑎2 + (𝑐 − 20)𝑎 + (𝑐2 − 20𝑐 + 128) ma co najmniej jedno miejsce zerowe (gdyż Δ𝑎 ≥ 0).
Wykresem funkcji 𝑓 jest parabola, której wierzchołek 𝑊 = (𝑝 , 𝑞) ma rzędną niedodatnią 𝑞 = − Δ⁄4.
Odcięta 𝑝 = − 𝑐−20⁄2 ∈ [16⁄3 , 8], a ponadto 𝑓(4) = 𝑐2 − 16𝑐 + 64 = (𝑐 − 8)2 ≥ 0.
Zatem 𝑓 ma miejsce zerowe w zbiorze [4 , +∞).
Podobnie argumentujemy, że funkcja 𝑔(𝑏) = 𝑏2 + (𝑐 − 20)𝑏 + (𝑐2 − 20𝑐 + 128) ma miejsce zerowe w przedziale [4 , +∞).
Zatem układ (1)–(2) ma rozwiązanie w zbiorze liczb rzeczywistych nie mniejszych od 4.
schemat punktacji
4 pkt – powołanie się na odpowiednie własności funkcji 𝑓 prowadzące do wniosku, że układ (1)–(2) ma rozwiązanie w zbiorze liczb rzeczywistych nie mniejszych od 4.
3 pkt – przyjęcie założenia 𝑐 ∈ [4 , 28⁄3] i zbudowanie funkcji
𝑓(𝑎) = 𝑎2 + (𝑐 − 20)𝑎 + (𝑐2 − 20𝑐 + 128) dla podanego zakresu parametru 𝑐.
2 pkt – obliczenie wyróżnika równania i podanie argumentacji prowadzącej do wniosku 𝑐 ∈ [4 , 28⁄3].
1 pkt – przyjęcie założenia, że układ (1)–(2) ma rozwiązanie i zapisanie prawidłowego równania kwadratowego z niewiadomą 𝑎 (lub 𝑏) i parametrem 𝑐.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.