Odpowiedź:
Przykładowe pełne rozwiązania
Sposób 1.
Niech 𝑑1 będzie odległością (w km) zastępu „Tropiciele” od miejscowości 𝐴.
Wyznaczamy zależność 𝑑1 od czasu 𝑡 (w godzinach), jaki upłynął od chwili wyruszenia zastępu z miejscowości 𝐴:
𝑑1(𝑡) = 4𝑡 dla 𝑡 ∈ [0 , 5].
Niech 𝑑2 będzie odległością (w km) zastępu „Korsarze” od miejscowości 𝐴.
Wyznaczamy zależność 𝑑2 od czasu 𝑡 (w godzinach), jaki upłynął od chwili wyruszenia zastępu z miejscowości B:
𝑑2(𝑡) = 15 − 2𝑡 dla 𝑡 ∈ [0 , 15⁄2].
Odległość między zastępami badamy do momentu, gdy pierwszy z nich dotrze do celu. Odległość 𝑑 między zastępami w chwili 𝑡 jest równa
dla 𝑡 ∈ [0 , 5]Badamy, dla jakiego argumentu 𝑡 ∈ [0 , 5] funkcja 𝑑 osiąga wartość najmniejszą.
Ponieważ funkcja 𝑔(𝑥) = √𝑥 jest funkcją rosnącą w przedziale [0 , +∞), więc funkcja 𝑑 osiąga wartość najmniejszą dla takiego argumentu, dla którego funkcja 𝑓 określona wzorem
𝑓(𝑡) = 16𝑡2 + (15 − 2𝑡)2 = 20𝑡2 − 60𝑡 + 225 dla 𝑡 ∈ [0 , 5]
osiąga wartość najmniejszą.
Korzystamy z własności funkcji kwadratowej i obliczamy argument, dla którego funkcja 𝑓 osiąga wartość najmniejszą:
𝑡 = 60⁄2 ⋅ 20 = 1,5 ∈ [0 , 5]
więc funkcja 𝑓 osiąga wartość najmniejszą dla 𝑡 = 1,5. Zatem funkcja 𝑑 osiąga wartość najmniejszą dla argumentu 𝑡 = 1,5.
Odległość między zastępami harcerzy będzie najmniejsza o godzinie 10:30.
Sposób 2.
Niech 𝑑1 będzie odległością (w km) zastępu „Tropiciele” od miejscowości 𝐴.
Wyznaczamy zależność 𝑑1 od czasu 𝑡 (w godzinach), jaki upłynął od chwili wyruszenia zastępu z miejscowości 𝐴:
𝑑1(𝑡) = 4𝑡 dla 𝑡 ∈ [0 , 5].
Niech 𝑑2 będzie odległością (w km) zastępu „Korsarze” od miejscowości 𝐴.
Wyznaczamy zależność 𝑑2 od czasu 𝑡 (w godzinach), jaki upłynął od chwili wyruszenia zastępu z miejscowości 𝐵:
𝑑2(𝑡) = 15 − 2𝑡 dla 𝑡 ∈ [0 , 15⁄2].
Odległość 𝑑 między zastępami w chwili 𝑡 wynosi
dla 𝑡 ∈ [0 , 5] oraz
dla 𝑡 ∈ (5 ,15⁄2],przy czym przyjmujemy, że dla 𝑡 ∈ [5 , 15⁄2] „Tropiciele” znajdują się w miejscowości 𝐶.
Badamy, dla jakiego argumentu 𝑡 ∈ [0 , 15⁄2] funkcja 𝑑 osiąga wartość najmniejszą.
Obliczamy pochodną funkcji 𝑑:
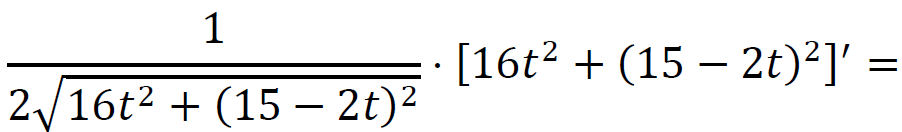
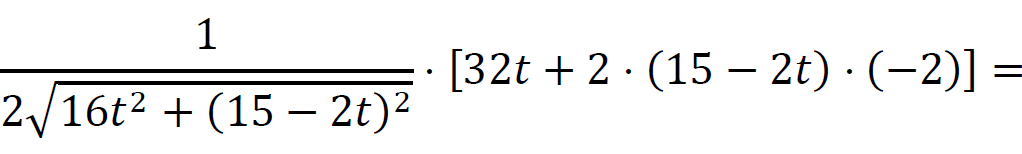
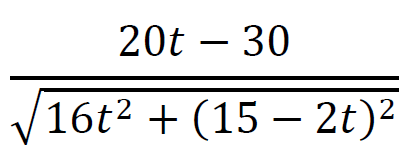dla 𝑡 ∈ [0 , 5] oraz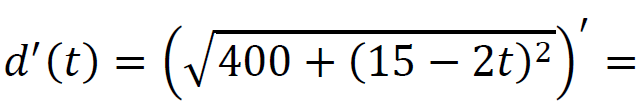
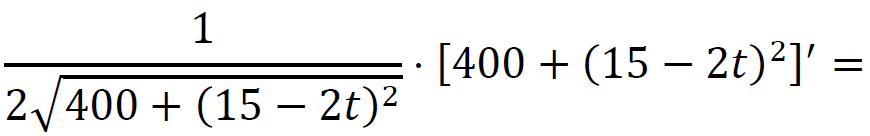
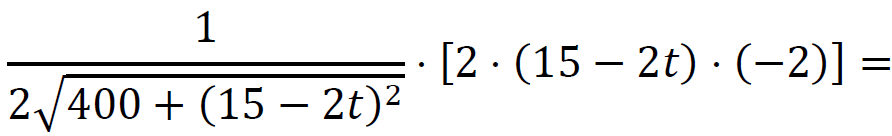
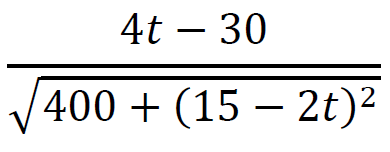dla 𝑡 ∈ (5 , 15⁄2].Wyznaczamy miejsca zerowe pochodnej funkcji 𝑑:
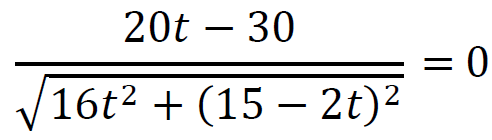
𝑡 = 3⁄2 ∈ [0 , 5]
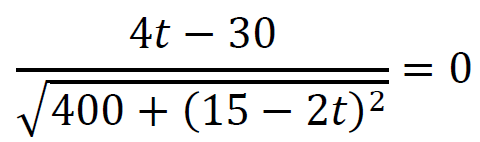
𝑡 = 15⁄2 ∈ (5 , 15⁄2]
Badamy monotoniczność funkcji 𝑑.
Ponieważ
𝑑′(𝑡) > 0 dla 𝑡 ∈ (3⁄2 , 5]
𝑑′(𝑡) < 0 dla 𝑡 ∈ [0 , 3⁄2) oraz dla 𝑡 ∈ (5 , 15⁄2)
więc
funkcja 𝑑 jest rosnąca w przedziale [3⁄2 , 5]
funkcja 𝑑 jest malejąca w przedziałach [0 , 3⁄2] oraz [5 , 15⁄2].
Ponadto 𝑑(3⁄2) = √180 oraz 𝑑(15⁄2) = √400. Zatem funkcja 𝑑 osiąga wartość najmniejszą dla 𝑡 = 1,5.
Odległość między zastępami harcerzy będzie najmniejsza o godzinie 10:30.
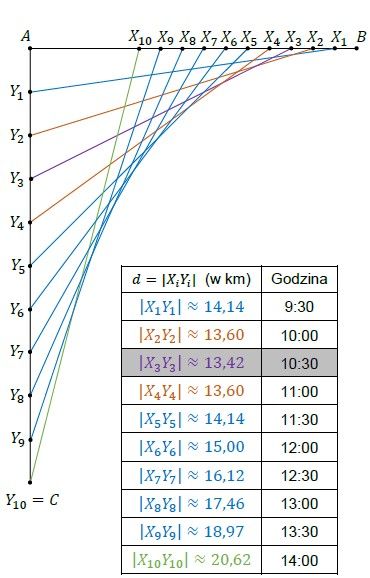
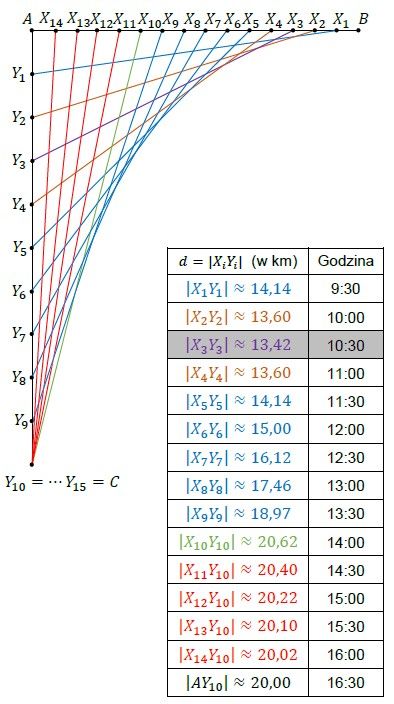
Poniżej przedstawiono ilustrację geometryczną do sposobów 1. (wyżej) oraz 2. (niżej).
Punkty 𝑋𝑖 odpowiadają położeniom zastępu „Korsarze” po kolejnych półgodzinnych odstępach czasu, licząc od momentu wyruszenia z miejscowości 𝐵.
Punkty 𝑌𝑖 odpowiadają położeniom zastępu „Tropiciele” po kolejnych półgodzinnych odstępach czasu, licząc od momentu wyruszenia z miejscowości 𝐴.
schemat punktacji
dla rozwiązania sposobem 1.
4 pkt – prawidłowa metoda wyznaczenia chwili, w której odległość między zastępami będzie najmniejsza i prawidłowa odpowiedź.
3 pkt – uzasadnienie, że odległość 𝑑 jest najmniejsza wtedy, gdy wyrażenie podpierwiastkowe 20𝑡2 − 60𝑡 + 225 jest możliwie najmniejsze oraz podanie zakresu zmienności 𝑡.
2 pkt – wyrażenie odległości 𝑑 między zastępami za pomocą czasu 𝑡, jaki upłynął od momentu wyruszenia zastępów.
1 pkt – wyrażenie odległości poszczególnych zastępów od miejscowości 𝐴 za pomocą czasu, jaki upłynął od momentu wyruszenia zastępów.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.
dla rozwiązania sposobem 2.
4 pkt – uzasadnienie (np. poprzez zbadanie monotoniczności), że dla 𝑡 = 1,5 funkcja 𝑑(𝑡) osiąga minimum globalne i podanie prawidłowej odpowiedzi.
3 pkt – podanie dziedziny funkcji 𝑑(𝑡), obliczenie pochodnej funkcji 𝑑(𝑡) i znalezienie punktów krytycznych.
2 pkt – wyrażenie odległości 𝑑 między zastępami za pomocą czasu 𝑡, jaki upłynął od momentu wyruszenia zastępów.
1 pkt – wyrażenie odległości poszczególnych zastępów od miejscowości 𝐴 za pomocą czasu, jaki upłynął od momentu wyruszenia zastępów.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.