Odpowiedź:
Przykładowe pełne rozwiązanie
Dochód 𝑍 firmy to przychód 𝑅 pomniejszony o koszty 𝐾.
Ponieważ przychód wyraża się zależnością 𝑅 = 𝑄 ⋅ 𝑃, więc
𝑅(𝑄) = 90𝑄 − 0,1𝑄2
Wyznaczamy zależność dochodu od wielkości produkcji:
𝑍(𝑄)=𝑅(𝑄)−𝐾(𝑄)
𝑍(𝑄) = −0,002𝑄3 − 1,1𝑄2 + 60,0015𝑄 − 50
W celu znalezienia optymalnej wielkości produkcji, przy której dochód jest możliwie największy, należy zbadać funkcję 𝑍.
Obliczamy pochodną funkcji 𝑍 i miejsca zerowe pochodnej:
𝑍′(𝑄) = −0,006𝑄2 − 2,2𝑄 + 60,0015 dla 𝑄 ∈ [0 , 900]
𝑍′(𝑄) = 0
−0,006𝑄2 − 2,2𝑄 + 60,0015 = 0 i 𝑄 ∈ [0 , 900]
Δ = (−2,2)2 − 4 ⋅ (−0,006) ⋅ 60,0015 = 6,280036
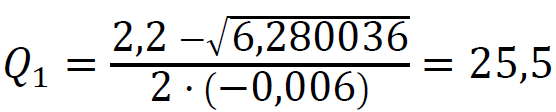(𝑄2 < 0)Ponieważ:
𝑍′(𝑄) > 0 dla 𝑄 ∈ [0 , 𝑄1]
𝑍′(𝑄) < 0 dla 𝑄 ∈ [𝑄1 , 900]
więc
funkcja 𝑍 jest rosnąca w przedziale [0 , 𝑄1]
funkcja 𝑍 jest malejąca w przedziale [𝑄1 , 900]
Zatem funkcja 𝑍 przyjmuje największą wartość dla argumentu 𝑄1 = 25,5.
Dochód firmy jest największy przy wielkości produkcji 25 500 sztuk.
schemat punktacji
4 pkt – prawidłowa metoda wyznaczenia wielkości produkcji gwarantującej maksymalny dochód i prawidłowy wynik zaokrąglony z podaną dokładnością.
3 pkt – znalezienie ekstremów lokalnych funkcji dochodu 𝑍(𝑄).
2 pkt – zapisanie dochodu w zależności od 𝑄.
1 pkt – zapisanie przychodu w zależności od 𝑄.
0 pkt – rozwiązanie, w którym zastosowano niepoprawną metodę, albo brak rozwiązania.