Rozważmy dla przykładu jadącą ze stałą prędkością lokomotywę ciągnącą 3 wagony. Opisaną sytuację przedstawiono na uproszczonym rysunku.

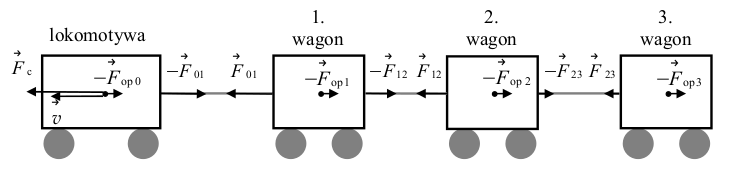
Przyjęto takie oznaczenia, że wektory wszystkich sił zwróconych zgodnie ze zwrotem prędkości pociągu mają znaki dodatnie, natomiast wektory wszystkich sił zwróconych przeciwnie niż zwrot prędkości pociągu mają znaki ujemne. Siłę ciągu lokomotywy oznaczono przez 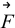_c.

Na lokomotywę działa siła oporu −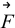_op0 , na 1. wagon −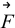_op1 , na 2. wagon −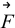_op2 , a na 3. −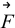_op3 . Odpowiednio oznaczono także siły oddziaływania między sąsiednimi wagonami, np. siłę oddziaływania między 1., a 2. wagonem −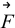₁₂ (siła działająca na 1. wagon) oraz 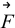₁₂ (siła działająca na 2. wagon). Analogicznie oznaczono siły oddziaływania w pozostałych połączeniach.

Wartości wyżej wymienionych sił oznaczmy tymi samymi symbolami bez wektorów, a więc: F _{op 0} , F _{op 1} , F _{op 2} , F _{op 3} , F ₀₁ , F ₁₂ , F ₂₃ , F _c .

Pociąg porusza się ze stałą prędkością, więc wypadkowa siła działająca na każdy wagon musi być równa 0. Oznacza to, że na przykład dla 2. wagonu zachodzi równość: F ₁₂ = F _{op 2} + F ₂₃ . Jak widać, wartość siły oddziaływania z wagonem znajdującym się bliżej lokomotywy jest większa niż wartość siły oddziaływania z wagonem znajdującym się dalej od lokomotywy.

Jak już zostało wspomniane, wypadkowa siła działająca na każdy wagon jest równa 0, a więc zachodzą następujące równości:

• dla 3. wagonu F ₂₃ = F _{op 3} ,

• dla 2. wagonu F ₁₂ = F _{op 2} + F ₂₃ , co po uwzględnieniu, że F ₂₃ = F _{op 3} można zapisać F ₁₂ = F _{op 2} + F _{op 3} ,

• dla 1. wagonu F ₀₁ = F ₁₂ + F _{op 1} , co po uwzględnieniu, że F ₁₂ = F _{op 2} + F _{op 3} można zapisać F ₀₁ = F _{op 1} + F _{op 2} + F _{op 3} .