W tekście do zadania podano wzór pozwalający obliczyć okres drgań wahadła fizycznego dla małych wychyleń:

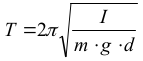
gdzie: I – moment bezwładności względem osi obrotu,

m – masa,

g – wartość przyspieszenia ziemskiego,

d – odległość środka ciężkości od osi obrotu.

Widać stąd, że im większe jest wyrażenie 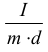, tym większy jest okres drgań wahadła. Dla punktualnie chodzącego zegara zwiększenie wyrażenia 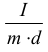spowoduje, że zegar będzie spóźniał się, zmniejszenie tego wyrażenia spowoduje, że będzie spieszył się, a jeżeli wyrażenie to pozostanie niezmienione, to zegar nadal będzie chodził punktualnie.

Do dalszych rozważań możemy przyjąć następujące oznaczenia:

m – masa wahadła przed doczepieniem magnesu,

d – odległość środka ciężkości wahadła od osi obrotu przed doczepieniem magnesu,

∆m – masa doczepionego magnesu,

d' – odległość środka ciężkości wahadła od osi obrotu po doczepieniu magnesu.

Wahadło zegara z zaznaczonymi środkami masy przed i po doczepieniu magnesu oraz odległościami od osi obrotu do obu środków masy zostało przedstawione na rysunku.

Oznaczając moment bezwładności wahadła przed doczepieniem magnesu przez I, można zapisać wyrażenie na moment bezwładności wahadła z doczepionym magnesem:

I' = I + ∆m ⋅ 0² = I

(masa punktowa doczepiona na osi obrotu nie zwiększa momentu bezwładności bryły względem tej osi). Masa wahadła z doczepionym magnesem jest równa: m' = m + ∆m.

Odległość środka masy wahadła z doczepionym magnesem od osi obrotu jest natomiast równa:

d' = ^{m ⋅ d + ∆m ⋅ 0}⁄_{m + ∆ m} = ^{m ⋅ d}⁄_{m + ∆m}

Zatem po doczepieniu magnesu wartość wyrażenia: