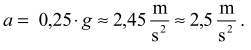Wskazówka:
Podczas hamowania powierzchnia wody jest nachylona pod pewnym kątem α w stosunku do poziomu. Sytuację taką pokazano w przekroju poprzecznym na rysunku 1.
Możemy przyjąć następujące oznaczenia sił działających na element masy wody ∆m znajdujący się na powierzchni: siła ciężkości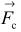
(jej wartość jest równa 
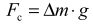), składowa siły ciężkości leżąca w płaszczyźnie rysunku równoległa do powierzchni wody 
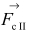(jej wartość jest równa 
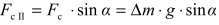), siła bezwładności 
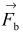(jej wartość jest równa 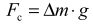), składowa siły bezwładności leżąca w płaszczyźnie rysunku równoległa do powierzchni wody 
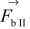(jej wartość jest równa 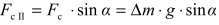), gdzie g jest wartością przyspieszenia ziemskiego, natomiast a - wartością opóźnienia pociągu podczas hamowania. Zachodzi równość: 
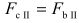zatem 
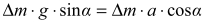, stąd 
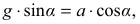a więc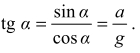 
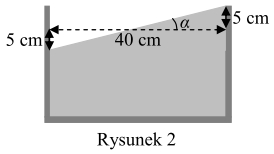
Jak można zobaczyć na rysunku 2, maksymalny kąt α nachylenia lustra wody w stosunku do poziomu, przy którym woda w całości pozostanie w akwarium, spełnia relację: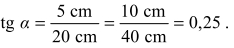
Tak więc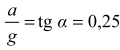
, a zatem maksymalna wartość opóźnienia pociągu podczas hamowania, przy którym woda w całości pozostanie w akwarium, jest równa:
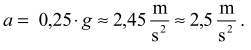
Możemy przyjąć następujące oznaczenia sił działających na element masy wody ∆m znajdujący się na powierzchni: siła ciężkości
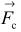(jej wartość jest równa 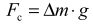), składowa siły ciężkości leżąca w płaszczyźnie rysunku równoległa do powierzchni wody 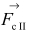(jej wartość jest równa 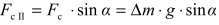), siła bezwładności 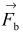(jej wartość jest równa 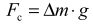), składowa siły bezwładności leżąca w płaszczyźnie rysunku równoległa do powierzchni wody 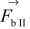(jej wartość jest równa 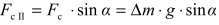), gdzie g jest wartością przyspieszenia ziemskiego, natomiast a - wartością opóźnienia pociągu podczas hamowania. Zachodzi równość: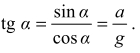 zatem , stąd a więc Jak można zobaczyć na rysunku 2, maksymalny kąt α nachylenia lustra wody w stosunku do poziomu, przy którym woda w całości pozostanie w akwarium, spełnia relację:
Tak więc
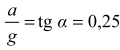, a zatem maksymalna wartość opóźnienia pociągu podczas hamowania, przy którym woda w całości pozostanie w akwarium, jest równa: