Wskazówka:
Oznaczmy wysokość, na jakiej spotkają się piłeczka i lampion przez h, natomiast czas lotu
piłeczki do góry, jako t. Piłeczka porusza się w górę ruchem jednostajnie opóźnionym.
Drogę, jaką przebędzie ona do spotkania z lampionem, można zapisać równaniem:
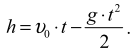
Lampion porusza się do góry ruchem jednostajnym, pamiętaj, że czas ruchu lampionu wynosi t1 + t, lampion leciał już do góry przez 4 s, zanim wyrzucono piłeczkę.
Drogę, jaką przebył lampion do momentu spotkania z piłeczką, zapisz jako:
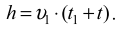
Ponieważ lampion i piłeczka mają spotkać się na wysokości h, otrzymujemy równanie:
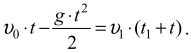
Ponieważ wszystkie wielkości fizyczne wyrażone są w podstawowych jednostkach układu SI, wstawimy do równania tylko ich wartości:
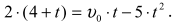
Piłeczka tylko raz spotka się z lampionem, jeżeli nastąpi to na maksymalnej wysokości, jaką ona osiągnie.
Czas wznoszenia piłeczki:
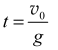
wstawiamy do wzoru:
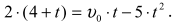
i otrzymujemy równanie na v0 , czyli:
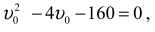
które ma rozwiązanie
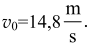
Teraz można sprawdzić. Czas wznoszenia piłeczki na maksymalną wysokość to 1,48 s. Maksymalna wysokość to h = 10,95 m Wysokość, na jakiej jest lampion w tej chwili, to h = 8 + 1,48 ⋅ 2 = 10,96 m, (czyli piłeczka spotka się z lampionem).
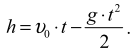
Lampion porusza się do góry ruchem jednostajnym, pamiętaj, że czas ruchu lampionu wynosi t1 + t, lampion leciał już do góry przez 4 s, zanim wyrzucono piłeczkę.
Drogę, jaką przebył lampion do momentu spotkania z piłeczką, zapisz jako:
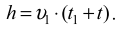
Ponieważ lampion i piłeczka mają spotkać się na wysokości h, otrzymujemy równanie:
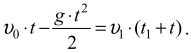
Ponieważ wszystkie wielkości fizyczne wyrażone są w podstawowych jednostkach układu SI, wstawimy do równania tylko ich wartości:
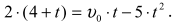
Piłeczka tylko raz spotka się z lampionem, jeżeli nastąpi to na maksymalnej wysokości, jaką ona osiągnie.
Czas wznoszenia piłeczki:
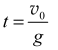
wstawiamy do wzoru:
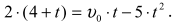
i otrzymujemy równanie na v0 , czyli:
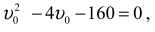
które ma rozwiązanie
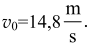
Teraz można sprawdzić. Czas wznoszenia piłeczki na maksymalną wysokość to 1,48 s. Maksymalna wysokość to h = 10,95 m Wysokość, na jakiej jest lampion w tej chwili, to h = 8 + 1,48 ⋅ 2 = 10,96 m, (czyli piłeczka spotka się z lampionem).