Wskazówka:
Na rysunku zaznaczono siły działające na wiadro i linkę,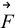 
g oznacza ciężar wiadra z wodą, natomiast N to siła naciągu linki. Wiadro z wodą porusza się w dół ruchem jednostajne przyspieszonym.
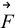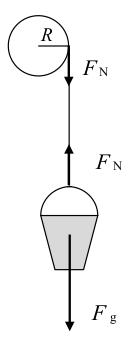
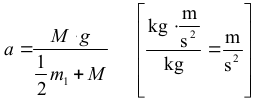
g oznacza ciężar wiadra z wodą, natomiast N to siła naciągu linki. Wiadro z wodą porusza się w dół ruchem jednostajne przyspieszonym.Wypadkowa siła działająca na wiadro ma wartość Fw = Fg − FN.
Z II zasady dynamiki Fw = M ⋅ a, gdzie M to masa wiadra z wodą. Wobec tego M ⋅ a = Fg − FN.
Krążek obraca się pod wpływem momentu siły 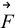N. Wartość momentu siły
wynosi MF = FN ⋅ R. Z II zasady dynamiki dla ruchu obrotowego można zapisać
wartość momentu siły MF = I ⋅ε , gdzie I to moment bezwładności krążka I = m1 ⋅ R2 , natomiast ε to wartość przyspieszenia kątowego krążka.
N. Wartość momentu siły
wynosi MF = FN ⋅ R. Z II zasady dynamiki dla ruchu obrotowego można zapisać
wartość momentu siły MF = I ⋅ε , gdzie I to moment bezwładności krążka I = m1 ⋅ R2 , natomiast ε to wartość przyspieszenia kątowego krążka. Z tego wynika, że I ⋅ε = FN ⋅ R.
W obliczeniach należy uwzględnić związek pomiędzy przyspieszeniem kątowym i liniowym a = R ⋅ε .
Z powyższych rozważań otrzymujemy układ równań:
M ⋅ a = Fg − FN (ruch postępowy wiadra)
I ⋅ε = FN ⋅ R (ruch obrotowy krążka)
I ⋅ε = FN ⋅ R (ruch obrotowy krążka)
I = ½ m1 ⋅ R2
a = R ⋅ε .
Rozwiązując powyższy układ równań, wyznaczamy przyspieszenie liniowe wiadra:
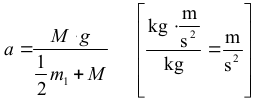
Po podstawieniu danych liczbowych otrzymujemy a = 7,5 m/s2 .