Wskazówka:
Odczytaj współrzędne punktów podanych na rysunku: A = (3,2), B = (5,-4), C = (–3,–1).
Korzystając ze wzoru na prostą przechodząca przez dwa punkty, wyznacz równania prostych
przechodzących przez każdą parę punktów.
Prosta AC ma równanie:
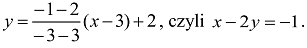
Prosta AB ma równanie:
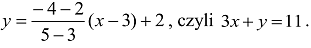
Prosta BC ma równanie:
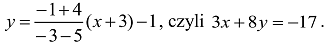
Ponieważ żadna z tych prostych nie jest równoległa do osi Oy, to możesz również skorzystać
z postaci kierunkowej prostej i po podstawieniu dwóch punktów wyznaczyć jej równanie. Np.
prosta AC ma równanie y = ax+b.
Podstawiasz współrzędne obu punktów:
2 = 3a+b i –1= –3a+b.
Stad a = b = ½.
Zatem równanie przybiera postać
y = ½ x+½, stad 2y = x+1, czyli x–2y = -1.
Mając wszystkie trzy proste, sprawdź, który z podanych w odpowiedzi układów zawiera te równania.