Wskazówka:
Czy wiesz, jak może wyglądać wykres funkcji kwadratowej, której zbiorem rozwiązań nierówności
ƒ(x)< 0 są liczby rzeczywiste z przedziału (1,5) ?
Aby rozwiązać zadanie, naszkicuj wykres funkcji y = –ƒ(x+3) .
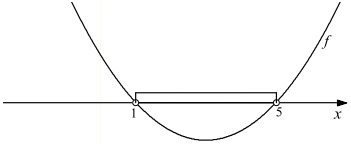
Z podanego wzoru wynika, że należy wykres funkcji ƒ przesunąć w lewo wzdłuż osi Ox o trzy
jednostki. Miejscami zerowymi będą odpowiednio liczby x = –2 i x = 2.
Drugą czynnością będzie przekształcenie wykresu funkcji y = ƒ(x+3) przez symetrię względem osi Ox. Zauważ, że to przekształcenie zmienia kierunek ramion paraboli, ale nie zmienia punktów leżących na osi Ox, więc liczby x = –2 i x = 2 są miejscami zerowymi funkcji y = ƒ(x+3) .