Wskazówka:
Miejscami zerowymi funkcji ƒ są liczby 1 oraz 3, więc osią symetrii paraboli, która jest wy
kresem tej funkcji, jest prosta x = 2. Na tej prostej leży wierzchołek paraboli będącej wykresem funkcji ƒ. Zastanów się, jakiego przesunięcia wykresu funkcji ƒ należy dokonać, aby
wierzchołek przesuniętej paraboli leżał na osi Oy.
Zapisz wzór funkcji g w postaci iloczynowej
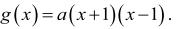
Następnie wykorzystaj fakt, że punkt (–2,–3) leży na wykresie funkcji g.
Możesz sporządzić rysunek i na jego podstawie ustalić, że należy wykonać przesunięcie wy
kresu funkcji ƒ o dwie jednostki w lewo (wzdłuż osi Ox); to oznacza, że wszystkie punkty,
które leżą na wykresie funkcji ƒ, zostaną w ten sposób przesunięte.
Znajdź współrzędne obrazu punktu (0,–3) i miejsc zerowych po przesunięciu.
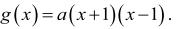
Następnie wykorzystaj fakt, że punkt (–2,–3) leży na wykresie funkcji g.