Zgodnie z treścią zadania sporządź w jednym układzie współrzędnych
wykresy funkcji
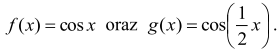
Czy wiesz, jak na podstawie wykresu funkcji ƒ narysować wykres funkcji g? Najpierw należy wyznaczyć okres podstawowy funkcji
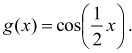
Jeśli nie wiesz, jak to zrobić, to przypomnę, że okresem podstawowym funkcji
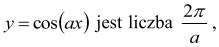
oczywiście gdy a≠0.
Zapewne okres
otrzymanej przez ciebie funkcji jest dwukrotnie większy niż okres
funkcji cosinus. Oznacza to, że wykres funkcji cosinus należy dwukrotnie
„rozciągnąć” wzdłuż osi Ox. Punktem wykresu, który nie zmieni położenia, jest
(0,1). Jak teraz na podstawie wykresów funkcji ƒ i g rozwiązać równanie
Należy odczytać z układu współrzędnych argumenty, dla których obie funkcje osiągają tę samą wartość, czyli argumenty punktów przecięcia się tych wykresów.
Następnym etapem jest algebraiczne rozwiązanie równania
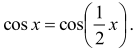
Skorzystaj ze wzoru na różnicę cosinusów i zapisz równanie w postaci
iloczynowej. Pamiętaj o okresowości funkcji y = sinx. Zapisz odpowiedź w najprostszej
postaci.
Czy w metodzie graficznej i algebraicznej udało ci się otrzymać ten sam zbiór rozwiązań?