Wskazówka:
Zauważ, że nie możesz bezpośrednio skorzystać z twierdzenia o granicy różnicy ciągów, gdyż ciągi określone wzorami
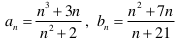
nie są zbieżne do granicy skończonej.
Wystarczy jednak wykonać działania na ułamkach i zapisać różnicę tych ciągów w postaci jednego ułamka algebraicznego. Teraz możesz zapisać otrzymany ułamek, np. dzieląc jego licznik i mianownik przez największą potęgę, w jakiej zmienna n występuje w mianowniku (wtedy ułamek nie zmienia wartości). Możesz teraz wykorzystać twierdzenia o działaniach na granicach ciągów zbieżnych do granic skończonych.
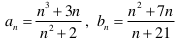
nie są zbieżne do granicy skończonej.
Wystarczy jednak wykonać działania na ułamkach i zapisać różnicę tych ciągów w postaci jednego ułamka algebraicznego. Teraz możesz zapisać otrzymany ułamek, np. dzieląc jego licznik i mianownik przez największą potęgę, w jakiej zmienna n występuje w mianowniku (wtedy ułamek nie zmienia wartości). Możesz teraz wykorzystać twierdzenia o działaniach na granicach ciągów zbieżnych do granic skończonych.