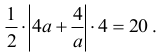Zapisz warunek prostopadłości dla danych prostych w postaci ogólnej i zauważ, że zmienną a możesz wyłączyć przed nawias. Otrzymane równanie ma dwa rozwiązania. Jakie? Sprawdź, że dla jednego z tych rozwiązań odpowiednie proste nie tworzą trójkąta (dwa boki byłyby wówczas równoległe).

Dla otrzymanego rozwiązania (odpowiedniej wartości parametru) zapisz równania obu prostych. Jakie są współrzędne punktów wspólnych tych prostych i osi Oy? Sprawdź, że odległość tych punktów, która jest długością podstawy odpowiedniego trójkąta, jest równa

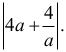
Zapisz i rozwiąż układ równań tych prostych. Sprawdź, że jedynym jego rozwiązaniem jest punkt (4,0).

Zauważ, że warunki postawione w treści zadania prowadzą do równania