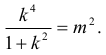Wskazówka:
Zauważ, że prosta styczna do okręgu ma z nim dokładnie jeden punkt wspólny. Ustal teraz,
dla jakich k i l prosta y = kx + l ma jeden punkt wspólny z okręgiem (x – k)2 + (y – l)2 = m2 . Aby wyznaczyć ten punkt, możesz rozwiązać układ równań (równanie prostej i równanie
okręgu). Po przekształceniu otrzymasz równanie kwadratowe z niewiadomą x. Posiada ono
jedno rozwiązanie, gdy wyróżnik trójmianu jest równy zero. Zapisz odpowiednie równanie.
Po przyrównaniu go do zera otrzymasz zależność między k i l:
(–2k)2 – 4(1 + k2)(k2 – m2) = 0
Przekształć to równanie do postaci