Losujemy jednocześnie trzy liczby z danego zbioru. Zastanów się, czym jest pojedyncze zdarzenie elementarne, a następnie wprowadź oznaczenia, na przykład niech A oznacza zdarzenie polegające na tym, że wśród wylosowanych liczb będzie liczba 4, a B – zdarzenie polegające na tym, że suma wylosowanych liczb będzie parzysta. Twoim zadaniem jest obliczenie prawdopodobieństwa warunkowego w modelu klasycznym



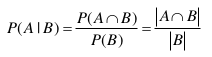
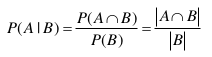
Oblicz moc zdarzenia B. Pomyśl, kiedy suma trzech liczb jest parzysta? Będą dwie możliwości. Teraz wyznacz liczbę zdarzeń elementarnych sprzyjających zajściu zdarzenia A∩B – suma trzech liczb jest parzysta i jednocześnie wśród nich jest liczba 4. W tym przypadku również będą dwie możliwości. Oblicz moc zdarzenia A∩B i oblicz prawdopodobieństwo warunkowe.