Obliczenie odsetka (procentu) cząsteczek CO₂ i H₂ , które uległy przekształceniu w CO i H₂O wymaga obliczenia liczby cząsteczek CO i H₂O, powstałych w wyniku reakcji. Dobrze jest zauważyć, że mikroskopowa wielkość, jaką jest liczba cząsteczek substancji, jest wprost proporcjonalna do makroskopowej wielkości określającej liczność materii, czyli liczby moli substancji. Spostrzeżenie to pozwala na wykonywanie obliczeń z zastosowaniem liczby moli, której nie trzeba przeliczać na liczbę cząsteczek. Punktem wyjścia do rozwiązania zadania jest równanie reakcji i wyrażenie na jej stężeniową stałą równowagi, ponieważ dysponujemy informacją o wartości tej stałej w temperaturze, w której reakcja była prowadzona. Stężeniowa stała równowagi jest ilorazem 2 iloczynów stężeń molowych w stanie równowagi: w liczniku są to stężenia produktów, a w mianowniku – stężenia substratów reakcji, wszystkie w pierwszej potędze. Jeżeli uwzględnimy fakt, że reakcja przebiegała w fazie gazowej w zamkniętym reaktorze o stałej pojemności, stwierdzimy, że w wyrażeniu na stałą równowagi stężenia molowe substancji w stanie równowagi można zastąpić liczbą moli poszczególnych substancji w stanie równowagi:

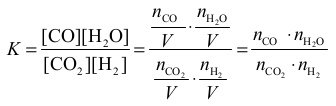
Analiza równania reakcji pozwala stwierdzić, że liczba moli powstałego CO jest równa liczbie moli H₂O i jest ona także liczbą moli tych substancji w stanie równowagi – w mieszaninie początkowej substancji tych nie było. Liczba moli w stanie równowagi substratów reakcji (CO₂ i H₂) to początkowa liczba moli tych substancji (równa 2 mole) pomniejszona o liczbę moli, która uległa reakcji. Ten ubytek CO₂ i H₂ jest równy liczbie moli otrzymanych CO i H₂O. Widzimy więc, że nasz problem sprowadza się do obliczenia niewiadomej (x), którą jest liczba moli produktów (a zarazem ubytek liczby moli substratów). Dzięki wyrażeniu na stałą równowagi reakcji i znajomości jej wartości otrzymujemy równanie z jedną niewiadomą:

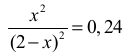
które sprowadzamy do postaci 0,76x² + 0,96x − 0,96 = 0 .