Aby wykazać, że po zmieszaniu roztworów w zlewce wytrącił się osad, należy obliczyć lokalny iloczyn I_L = [Ca²⁺] ⋅ [F⁻]² i porównać go z iloczynem rozpuszczalności fluorku wapnia. Jeżeli lokalny iloczyn stężeń jonów wapnia i jonów fluorkowych do drugiej potęgi okaże się większy od iloczynu rozpuszczalności fluorku wapnia, będzie to oznaczać, że osad się wytrącił. Najpierw należy obliczyć liczbę moli chlorku wapnia, wiedząc, że:

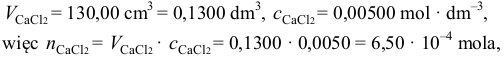
następnie należy obliczyć liczbę moli fluorku sodu, wiedząc, że:

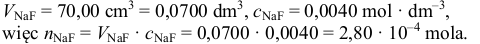
Następnie musimy zauważyć, że – zgodnie z równaniami dysocjacji jonowej:

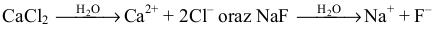
– liczba moli kationów wapnia jest równa liczbie moli chlorku wapnia (molowy stosunek stechiometryczny 1 : 1) i liczba moli anionów fluorkowych jest równa liczbie moli fluorku sodu (molowy stosunek stechiometryczny = 1 : 1), dlatego

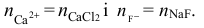
Powinniśmy także zauważyć, że objętość nowopowstałego roztworu będzie równa sumie objętości roztworów zmieszanych ze sobą: V t = V CaCl 2 + V NaF = 0,200 dm 3 . Mając liczbę moli kationów wapnia i anionów fluorkowych oraz objętość nowopowstałego roztworu, możemy obliczyć stężenia reagujących ze sobą jonów w tym roztworze zaraz po zmieszaniu roztworów początkowych:

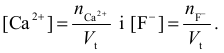
Następnie zapisujemy równanie reakcji wytracania osadu fluorku wapnia: Ca²⁺ + 2F^– → CaF₂↓ oraz wyrażenie na lokalny iloczyn I_L=[Ca²⁺]⋅[ F⁻]² , pamiętając, że stężenie jonów fluorkowych występuje w potędze drugiej ze względu na prawo działania mas (wykładnik w potędze stężenia jest równy współczynnikowi stechiometrycznemu reagenta). Po obliczeniu wartości iloczynu lokalnego:

I_L=[Ca²⁺]⋅[ F⁻]² = 3,25 ⋅ 10⁻³ ⋅ (1 ,40 ⋅ 10⁻³) 2 = 6,37 ⋅ 10⁻⁹

stwierdzamy, że jego wartość jest większa niż wartość iloczynu rozpuszczalności K_so(CaF2)=3,16⋅10⁻¹¹ . Jest to dowód na wytrącenie się osadu w zlewce.