Najpierw rozwiążemy drugą część zadania, czyli podamy zależność rekurencyjną, określającą złożoność elementarną. Na podstawie tej zależności łatwo rozwiążemy pierwszą część zadania.

Ponieważ wykonania wynik(0), wynik(1) oraz wynik(2) kończą się natychmiastowym zwróceniem wyniku, każdemu z nich odpowiada dokładnie jedno wykonanie elementarne. To daje nam warunek brzegowy rekurencji:

E(0) = E(1) = E(2) = 1.

Natomiast dla każdego i>2 sytuacja jest zależna od parzystości liczby i:

• Dla parzystych i>2 wykonanie wynik(i) pociąga za sobą wykonanie wynik(i-1) oraz wynik(i-3). Zgodnie z przyjętymi oznaczeniami wykonanie wynik(i-1) wymaga E(i-1) wykonań elementarnych. Analogicznie wynik(i-3) wymaga E(i-3) wykonań elementarnych. Zatem wynik(i) pociąga za sobą E(i-1) + E(i-3) wykonań elementarnych. 

Stąd:

E(i) = E(i-1) + E(i-3) dla parzystego i>2.

• Z kolei wykonanie wynik(i) dla nieparzystego i > 2 powoduje tylko wykonanie wynik(i-1). Stąd:

E(i) = E(i-1) dla nieparzystego i>2.

Ostatecznie:

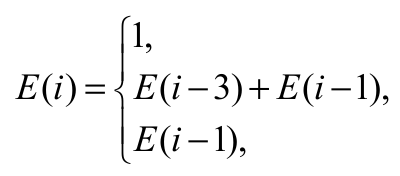
dla i ∈ {0,1,2},

dla parzystego i > 2,

dla nieparzystego i > 2,

Znając rekurencyjną formułę dla wyznaczania E(i), możemy wypełnić podaną w zadaniu tabelkę, stosując tę formułę dla kolejnych i=3,4, .,10, podobnie jak w zadaniu 1 robiliśmy to dla funkcji wynik. Drobna różnica polega jedynie na tym, że w zadaniu 1 formuła zapisana była w innej postaci, a mianowicie w postaci pseudokodu.