Rozważamy liczbę n, która jest potęgą dwójki. Zauważmy, że liczba wywołań rekurencyjnych jest równa liczbie wykonań instrukcji s ← (p+k) div 2. Te instrukcje wykonują się, gdy k ≠ p, czyli gdy w ciągu danych jest więcej niż 1 element. Musimy się zastanowić, ile razy odrzucamy połowę ciągu, tak aby w ciągu pozostał 1 element. Dla n = 8 = 2³ pierwsze wywołanie rekurencyjne zredukuje zakres poszukiwań do ciągu 4-elementowego (elementy ciągu od pierwszego do czwartego lub od piątego do ósmego). Po drugim wywołaniu analizujemy ciąg dwuelementowy. W trzecim wywołaniu sprawdzamy jeden element ciągu. Analogiczne rozważanie można przeprowadzić dla n = 16 = 2⁴ (wywołujemy funkcję F czterokrotnie), dla n = 32 = 2⁵ (wywołujemy funkcję F pięciokrotnie). Dla n = 2^k funkcja F będzie wywołana k razy, k = log₂ n. 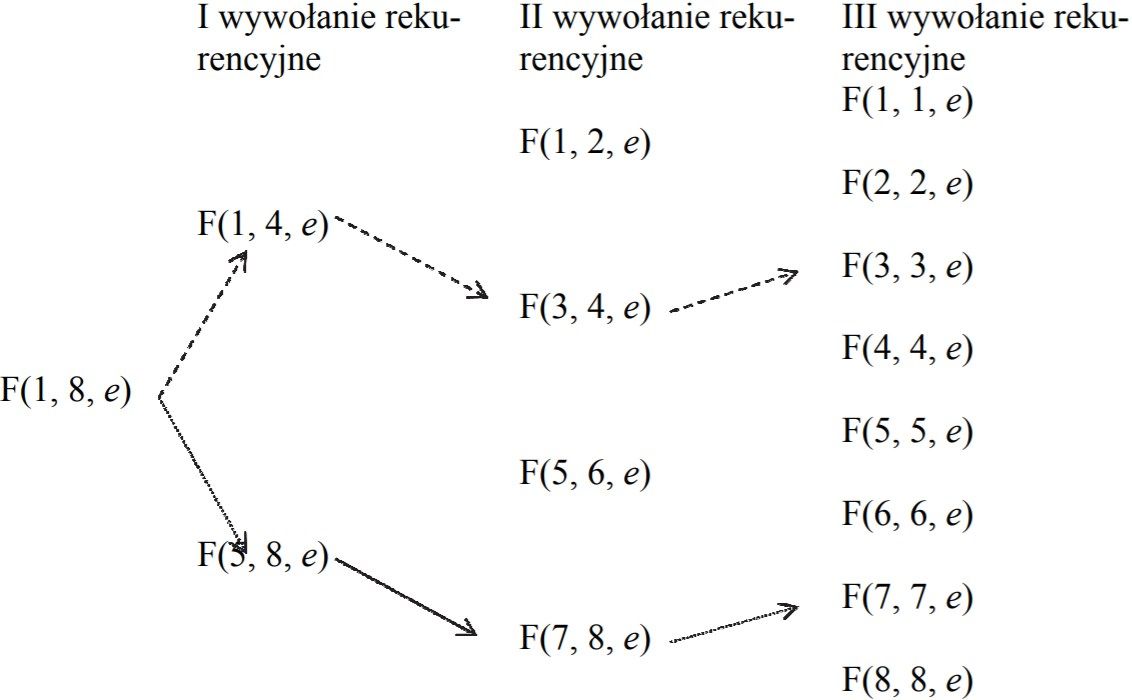Dla lepszego zrozumienia poniżej przedstawiono możliwe wywołania funkcji F(1, 8, e) oraz przykładowe ścieżki wywołań rekurencyjnych.