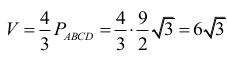Odpowiedź:
I sposób
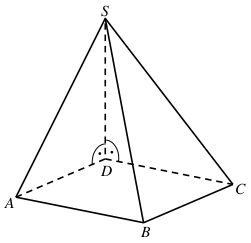
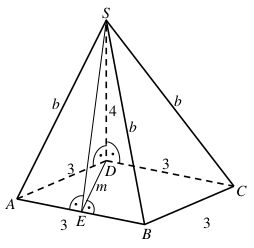
Przyjmijmy oznaczenia jak na rysunku.
Objętość tego ostrosłupa jest równa
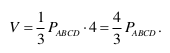
Zadanie sprowadza się więc do obliczenia pola rombu ABCD.
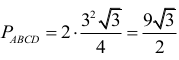
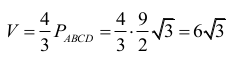
Poprowadźmy wysokość SE ściany bocznej ABS i przyjmijmy oznaczenia jak na rysunku.
Z twierdzenia Pitagorasa dla trójkąta ADS otrzymujemy
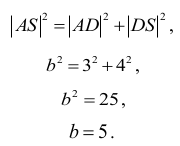
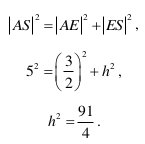
Trójkąt EDS jest prostokątny, gdyż krawędź DS jest prostopadła do płaszczyzny podstawy ostrosłupa. Z twierdzenia Pitagorasa dla tego trójkąta otrzymujemy
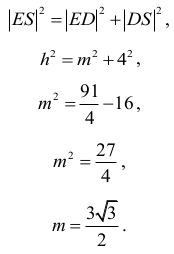
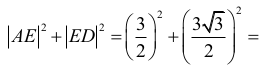
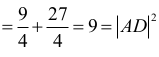
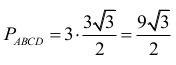
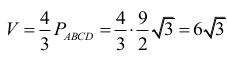
Przyjmijmy oznaczenia jak na rysunku.

Objętość tego ostrosłupa jest równa
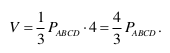
Zadanie sprowadza się więc do obliczenia pola rombu ABCD.
Ponieważ krawędź DS jest wysokością ostrosłupa, to trójkąty ADS, BDS i CDS są prostokątne, a DS jest wspólną przyprostokątną każdego z nich.
Ponieważ krawędzie boczne AS, BS
i CS mają tę samą długość, to trójkąty ADS, BDS i CDS mają równe przeciwprostokątne.
Zatem z twierdzenia Pitagorasa wynika, że równe są też przyprostokątne AD, BD i CD. To
oznacza, że przekątna BD rombu ABCD ma taką samą długość jak bok tego rombu, więc
trójkąty ABD i BCD są równoboczne. Pole rombu jest więc równe
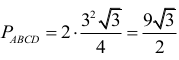
Objętość ostrosłupa jest zatem równa
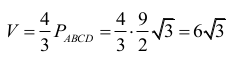
II sposób
Poprowadźmy wysokość SE ściany bocznej ABS i przyjmijmy oznaczenia jak na rysunku.

Z twierdzenia Pitagorasa dla trójkąta ADS otrzymujemy
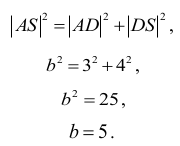
Ponieważ trójkąt ABS jest równoramienny, gdyż |AS| = |BS|, to spodek E tej wysokości jest środkiem podstawy AB tego trójkąta. Zatem
|AE| = ½ · 3 = 3⁄2
Z twierdzenia Pitagorasa dla trójkąta AES otrzymujemy
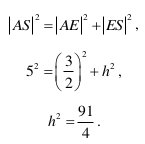
Trójkąt EDS jest prostokątny, gdyż krawędź DS jest prostopadła do płaszczyzny podstawy ostrosłupa. Z twierdzenia Pitagorasa dla tego trójkąta otrzymujemy
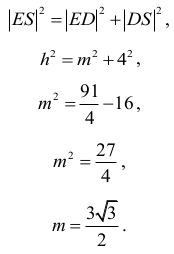
Zauważmy, że odcinek DE jest wysokością rombu ABCD opuszczoną z wierzchołka D na bok AB, gdyż
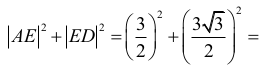
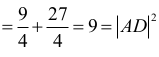
Zatem pole rombu ABCD jest równe
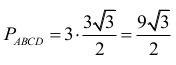
Objętość ostrosłupa jest zatem równa