Odpowiedź:
Przykładowe rozwiązanie
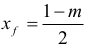
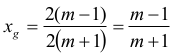
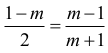
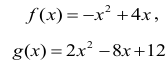
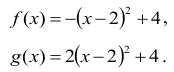
Niech punkt Wƒ = (xƒ , yƒ) będzie wierzchołkiem paraboli, która jest wykresem funkcji kwadratowej ƒ. Wtedy
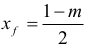
Analogicznie, niech punkt Wg = (xg , yg) będzie wierzchołkiem paraboli, która jest wykresem funkcji kwadratowej g. Wtedy
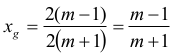
Oczywiście, ponieważ funkcja g jest kwadratowa, musi zachodzić warunek m ≠ -1.
Z warunków zadania wynika, że xg = xƒ , zatem
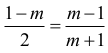
Ostatnie równanie można zapisać w postaci równoważnej
1 – m2 = 2(m –1)
czyli
(m –1)(m + 3) = 0
Jego rozwiązaniami są liczby 1 oraz -3.
Zauważmy, że dla m = 1 funkcja g byłaby określona wzorem g(x) = –2x2 – 4 , tym samym nie miałaby wartości najmniejszej.
Z kolei dla m = -3 otrzymujemy:
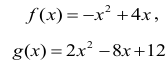
Zapisując otrzymane trójmiany w postaci kanonicznej, otrzymujemy:
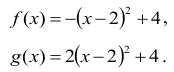
Stąd ƒ(x) ≤ g(x) dla każdej wartości x.
Uwaga:
Oczywiście g(x) – ƒ(x) = 3·(x – 2)2 ≥ 0 , co oznacza, że g(x) ≥ ƒ(x).