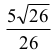Oznaczmy punkt przecięcia się odcinków DF i BG jako Q oraz

|∢ABG| = α,

|∢DQB| = β,

|DE| = |DG| = x

Trójkąty ADG i BEF są przystające, ponieważ są prostokątne i mają taką samą przyprostokątną (|GD| = |EF|), naprzeciw której znajdują się równe kąty (kąty przy podstawie trójkąta równoramiennego).

Naszkicujmy wysokość trójkąta CFG poprowadzoną z wierzchołka C — spodek tej wysokości oznaczmy jako P.

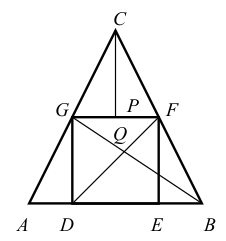
Wtedy trójkąty ADG oraz GPC są podobne, bo ich boki są odpowiednio równoległe. Pole trójkąta CFG (podzielonego odcinkiem CP na dwa przystające trójkąty: CGP i CFP) jest równe sumie pól przystających trójkątów ADG i BEF, zatem trójkąty ADG oraz GPC są przystające.W szczególności

|EB| = ½ |DE|

Ponieważ |∢EDF| = 45°

to 

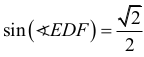
z kolei

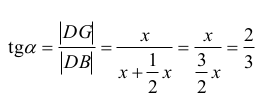
i kąt jest ostry, więc

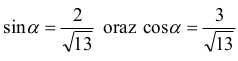
zatem

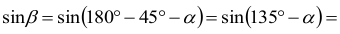
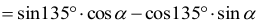
ale

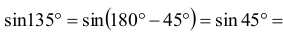
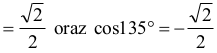
stąd

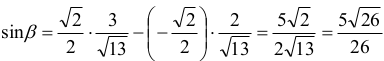
Pozostaje zauważyć, że kąt ostry, pod jakim przecinają się odcinki DF i BG, jest kątem przyległym do kąta β, zatem sinus kąta ostrego, pod jakim przecinają się odcinki DF i BG, jest równy