Zadanie 9.
W trójkąt równoramienny ABC wpisano kwadrat w taki sposób, że bok DE kwadratu zawiera się w podstawie AB trójkąta, a wierzchołki F i G kwadratu leżą odpowiednio na ramionach BC i AC trójkąta (zobacz rysunek).
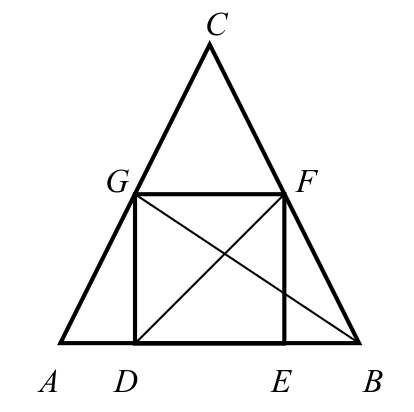
Pole trójkąta CFG jest równe sumie pól trójkątów ADG i BEF. Oblicz sinus kąta ostrego, pod jakim przecinają się odcinki DF i BG.
Ta odpowiedź nie jest sprawdzana automatycznie. Zobacz odpowiedź i oceń się samodzielnie.