Odpowiedź:
I sposób
Wyznaczamy środek i promień okręgu O1:
S1 = (3,0), r1 = 6.
Wyznaczamy środek i promień okręgu O2:
S2 = (0,m), r2 = |m|, gdzie m≠0.
Okręgi mają dokładnie jeden punkt wspólny, gdy są styczne.
Sytuacja pierwsza
Okręgi styczne zewnętrznie.
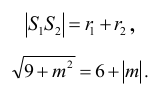
Przekształcamy równoważnie równanie:

Otrzymujemy równanie sprzeczne.
Zatem, nie istnieje taka wartość parametru m, dla której okręgi są styczne zewnętrznie.
Sytuacja druga
Okręgi styczne wewnętrznie.

Przekształcamy równoważnie równanie:

Dla

Wyznaczamy równanie prostej S1S2:

Zatem:
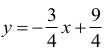
Dla
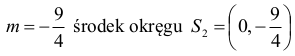
Wyznaczamy równanie prostej S1S2:
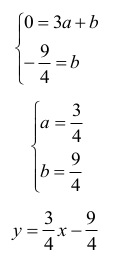
II sposób
Rozwiązujemy układ równań:
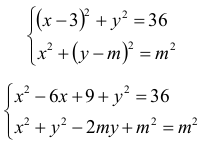
Odejmując równania stronami, otrzymujemy:
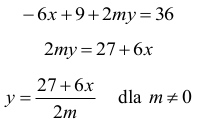
Otrzymujemy równanie:

Aby okręgi były styczne, równanie musi mieć dokładnie jedno rozwiązanie. Zatem wyróżnik równania Δ = 0.
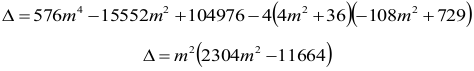
Otrzymujemy równanie:
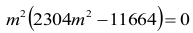
Stąd
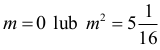
m = 0 — sprzeczne z założeniem
Zatem
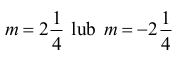
Dla
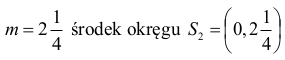
Wyznaczamy równanie prostej S1S2:
Dalsza część tak, jak w I sposobie.