Należy sprawdzić, czy pod działaniem siły 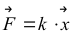 możliwe są wymienione ruchy.

Ruch nie może być jednostajny, ponieważ siły nie równoważą się.
Wartość siły nie jest stała, lecz zależy od współrzędnej położenia, czyli nie może to być ruch jednostajnie zmienny.
Wektor siły ma zwrot zgodny z wektorem położenia, dlatego nie może to być ruch harmoniczny.
Wartość siły rośnie proporcjonalnie do x , czyli rośnie także przyspieszenie klocka. Wektor siły ma zwrot zgodny z wektorem prędkości klocka. Z podanych ruchów może to być jedynie ruch przyspieszony.
Ponieważ wartość siły rośnie proporcjonalnie do x, to pracę tej siły można obliczyć, wstawiając do wzoru na pracę średnią wartość siły na odcinku ∆x:

F_sr = ½ ⋅ F = ½ ⋅ k ⋅ ∆x

skąd:

W = F_sr ⋅ ∆x = ½ ⋅ k ⋅ ∆x ⋅ ∆x = ½ ⋅ k ⋅ ∆x²

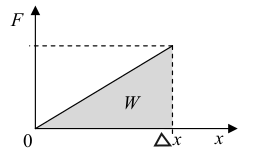
Pracę tej siły można także obliczyć jako pole figury pod wykresem zależności F(x).

Figura pod wykresem jest trójkątem, czyli:

W = ½ F ⋅ ∆x = ½ ⋅ k ⋅ ∆x ⋅ ∆x = ½ ⋅ k ⋅ ∆x²