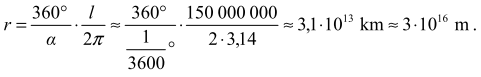Wskazówka:
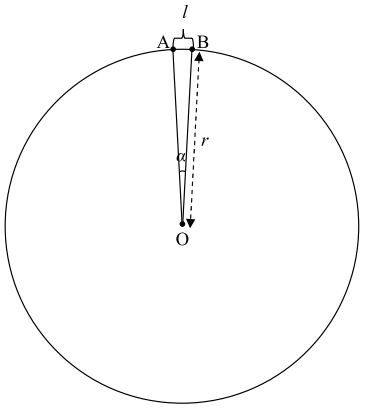
Rozważmy przedstawiony na poniższym rysunku okrąg o promieniu r. Jego środek znajduje
się w punkcie O. Na okręgu wybieramy punkty A i B takie, że kąt α między odcinkami AO
oraz BO jest bardzo mały. Można wtedy przyjąć, że długość odcinka AB jest równa
oznaczonej na rysunku symbolem l długości łuku między tymi punktami.
W tej sytuacji stosunek długości łuku AB do długości całego okręgu jest równy stosunkowi kąta α do pełnego kąta, co można zapisać następująco:
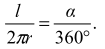
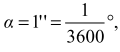
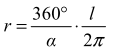
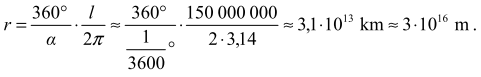

W tej sytuacji stosunek długości łuku AB do długości całego okręgu jest równy stosunkowi kąta α do pełnego kąta, co można zapisać następująco:
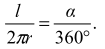
W tekście do zadania napisano, że 1 pc to odległość, dla której paralaksa heliocentryczna
położenia Ziemi widzianej prostopadle do płaszczyzny jej orbity wynosi , 1'' a więc
pod kątem 1'' z kierunku prostopadłego do płaszczyzny orbity Ziemi wokół Słońca
z odległości 1 pc widać byłoby promień orbity ziemskiej.
Przyjmując zatem, że l = 150 000 000 km (promień orbity ziemskiej równy połowie podanej
w tekście do zadania średnicy tej orbity),
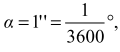
można obliczyć równą 1 pc odległość: