Aby obliczyć c, przyjrzyj się najpierw funkcji ƒ. Z postaci funkcji kwadratowej wynika, że jej wykresem jest parabola o ramionach skierowanych w dół. Taka funkcja największą wartość przyjmuje w wierzchołku. Ponieważ zbiorem wartości funkcji jest przedział (-∞,7⟩, to liczba 7 jest drugą współrzędną wierzchołka paraboli.

Oblicz pierwszą współrzędną p wierzchołka paraboli będącej wykresem funkcji

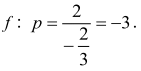
Wierzchołek paraboli ma współrzędne:

p = –3, q = 7, zatem ƒ(–3) = 7.

Stąd otrzymujesz równanie

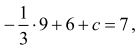
którego rozwiązaniem jest c = 4.