Wskazówka:
1. Zgodnie z podaną w treści zadania definicją, algorytm sprawdzania, czy dana liczba x
jest B-narcystyczna, można zrealizować w następujących dwóch krokach: Znajdź reprezentację
liczby x w systemie o podstawie B. Powiedzmy, że jest ona postaci
x = an-1Bn-1 + a(n-2)Bn-2 + ... + a1B + a0.
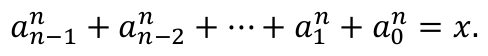
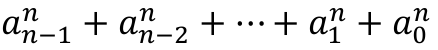
x = an-1Bn-1 + a(n-2)Bn-2 + ... + a1B + a0.
2. Sprawdź, czy
Pierwszy krok można rozwiązać, korzystając z tego, że cyfra a0 jest resztą z dzielenia liczby x przez B. Następne cyfry można wyznaczyć rekurencyjnie, po wykonaniu operacji x ←div(x,B). W ten sposób otrzymamy wszystkie cyfry w kolejności od a0 do an-1. Rekurencję tę należy zakończyć, gdy B = 0. W ten sposób otrzymamy również liczbę n, tzn. długość zapisu liczby x w systemie o podstawie B. Mając te informacje, przechodzimy do drugiego kroku. Jedną z możliwych jego realizacji jest napisanie do obliczania potęgi zk pomocniczej funkcji potega(z, k). Wówczas obliczanie sumy
można zrealizować za pomocą zwykłego sumowania kolejnych składników. Zauważmy, że sumowanie to można zorganizować w kolejności od 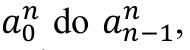 co oznacza postępowanie podobne do tego, jak w przypadku algorytmu wyznaczania reprezentacji liczby x w systemie o podstawie B:
co oznacza postępowanie podobne do tego, jak w przypadku algorytmu wyznaczania reprezentacji liczby x w systemie o podstawie B:
• wyznaczać kolejne cyfry a0, a1, ... , an-1,
• dla każdej cyfry ai obliczać 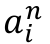 , korzystając z pomocniczej funkcji potega; sumując zarazem tak wyznaczone wartości n-tych potęg cyfr ai.
, korzystając z pomocniczej funkcji potega; sumując zarazem tak wyznaczone wartości n-tych potęg cyfr ai.
Poniżej prezentujemy fragment pseudokodu realizujący naszą strategię.
suma ← 0;
dopóki m>0 wykonuj
suma ← suma + potega( m mod B, n );m ← m div B;
Po obliczeniu tej sumy wystarczy sprawdzić, czy suma=x.